
来源:欧米伽未来研究所

人工智能与物理学:全面调查
摘要
揭示物理学机制正在推动人工智能(AI)发现的新范式。如今,物理学通过数据、知识、先验和规律,使我们能够在广泛的物质、能量和时空尺度上理解AI范式。同时,AI范式也汲取并引入物理学的知识和规律以促进自身的发展。这种利用物理科学启发AI的新范式就是人工智能的物理(PhysicsScience4AI,PS4AI)。虽然AI已经成为各个领域发展的驱动力,但在AI深度学习领域仍然存在一个难以解释的“黑箱”现象。本文将简要回顾相关物理学科(经典力学、电磁学、统计物理、量子力学)与AI之间的联系,重点讨论物理学科的机制及其如何启发AI深度学习范式,并简要介绍AI解决物理问题的一些相关工作。PS4AI是一个新的研究领域。在文章的结尾,我们总结了新物理启发AI范式面临的挑战,并展望下一代人工智能技术。本文旨在对物理启发的AI深度算法相关研究进行简要回顾,并通过阐明物理学的最新进展,激发未来的研究和探索。
目录



1 引言
人工智能包含了广泛的算法(Yang等,2023;LeCun等,1998;Krizhevsky等,2012;He等,2016)和用于大规模数据处理任务的建模工具(Sutskever等,2014)。海量数据和深度神经网络的出现为各个领域提供了优雅的解决方案。学术界也开始探索AI在各种传统学科中的应用,目标是促进AI的发展,同时进一步提升传统分析建模的可能性(Hsieh,2009;Ivezić等,2019;Karpatne等,2017,2018;Kutz,2017;Reichstein等,2019)。实现通用人工智能是人类一直追求的目标。尽管在过去的几十年里,AI取得了相当大的进展,但实现通用机器智能和类脑智能仍然困难重重(Jiao等,2016)。
目前,研究人员开始探索“AI + 物理”这一领域(Muther等,2023;Mehta等,2019)。当前研究的目标包括:(1)利用物理科学和人工智能的发现来研究大脑学习的基本原理;(2)利用AI促进物理学的发展;(3)应用物理科学来指导新AI范式的发展。我们选择性地回顾了AI与物理科学交叉领域的相关研究,包括物理洞察推动的AI概念与算法的发展、人工智能技术在多个物理领域中的应用,以及这两个领域的交叉点(Zdeborová,2020;Meng等,2022)。
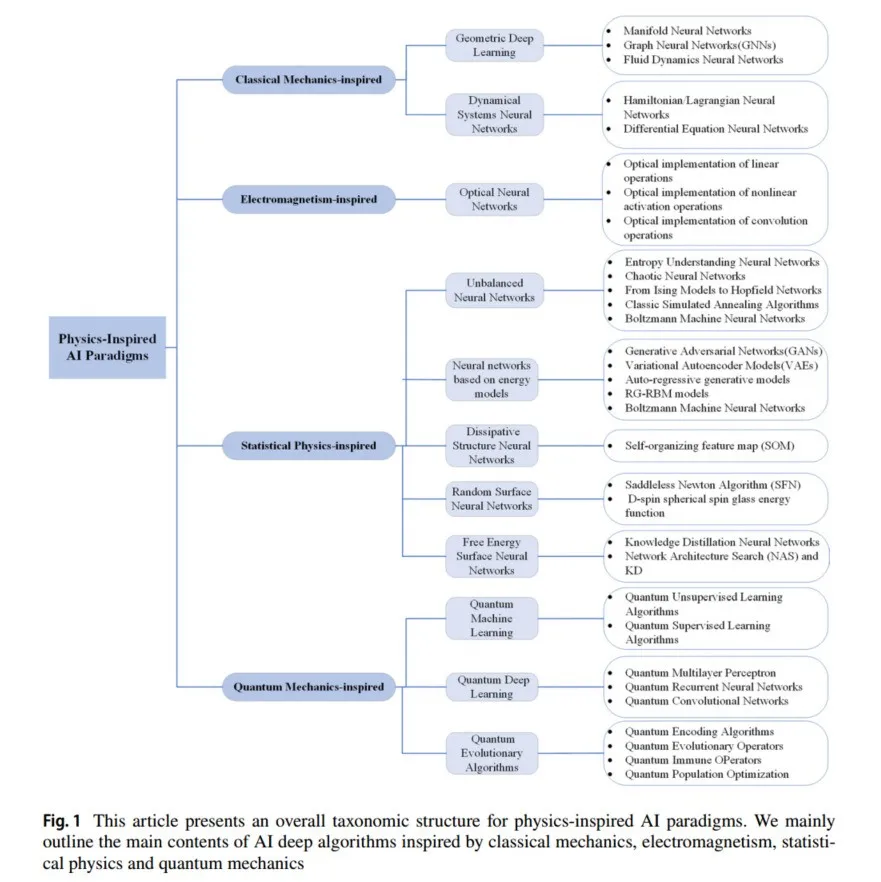
物理学 众所周知,物理学是一门自然科学,在认知客观世界中具有启发性作用,重点研究物质、能量、空间和时间,特别是它们各自的属性及其相互关系。广义上讲,物理学通过探索和分析自然界发生的现象来理解其规律。统计力学描述了神经网络在统计物理学中的理论进展(Engel,2001)。在漫长的历史中,物理知识(先验知识)已被收集、验证并整合到实用理论中。它是自然和人类行为规律在许多重要学科和工程应用中的简化归纳。如果能够适当结合先验知识与AI,则可以从稀疏的数据集中提取出更丰富和有效的特征信息,有助于提高网络模型的泛化能力和可解释性(Meng等,2022)。
人工智能 人工智能是一门研究和开发用于模拟和扩展人类大脑智能的理论和应用系统的学科。人工智能的目的是使机器能够模拟人类的智能行为(如学习、推理、思考、规划等)(Widrow和Lehr,1990),使机器具备智能并完成“复杂工作”。如今,人工智能在计算机领域受到了广泛关注,涉及机器视觉(Krizhevsky等,2012;Heisele等,2002)、自然语言处理(Devlin等,2018)、心理学(Rogers和Mcclelland,2004;Saxe等,2018)和教育学(Piech等,2015)等学科,是一门跨学科的学科。物理科学与深度学习的融合为理论科学提供了激动人心的前景,提供了对深度网络学习和计算能力的宝贵见解。
关系 物理学的发展是对自然的简化归纳,促进了人工智能中的类脑科学研究。而大脑对任何“经验”技术的感知接近于所谓的“物理感知”,物理学为当前人工智能研究开辟了新途径并提供了新工具(McCormick,2022)。在某种程度上,人工智能模型和物理模型都可以共享信息并预测复杂系统的行为(Tiberi等,2022),即它们共享某些方法和目标,但实现方式不同。因此,物理学应当理解自然机制,利用先验知识(Niyogi等,1998)、规律性和归纳推理来指导模型,而与模型无关的AI则应通过数据提取提供“智能”(Werner,2013)。
主要贡献 基于这些分析,本研究旨在对物理启发的AI深度学习领域进行全面回顾和分类,并总结未来急需解决的潜在研究方向和开放问题。本文的主要贡献总结如下:
全面性和可读性。本文全面回顾了400多个物理科学正在进展中的思想和物理启发的深度学习AI算法,并从经典力学、电磁学、统计物理和量子力学四个方面总结了现有的物理启发学习和建模研究。
启发性。文章总结了人工智能技术解决物理科学问题的最新进展。最后,在新一代深度学习人工智能算法中,我们分析了AI与物理学之间的展望与意义。
深入分析。本文回顾了需要解决的开放问题,以促进未来的研究和探索。
在本综述中,我们试图对深度学习人工智能与物理学的不同交叉点进行一致的回顾。本文的其余部分组织如下:第2章介绍了从经典力学角度启发的人工智能算法及其如何解决物理问题。第3章简要回顾了电磁学启发的人工智能算法及其在电磁学中的应用。第4章和第5章分别概述了统计物理学和量子力学启发的AI算法及其应用。第6章探讨了当前AI与物理学交叉点面临的潜在应用和挑战。第7章是本文的结论。
2 由经典力学启发的深度神经网络范式
本节我们将简要介绍几何深度学习中的流形、图和流体动力学,以及动态神经网络系统中Hamiltonian/Lagrangian和微分方程求解器的基础知识。然后解释与其相关的工作,最后介绍图神经网络的深度学习方法来解决物理问题。我们在表1中总结了本节的结构和代表性方法的概述。
2.1 几何深度学习
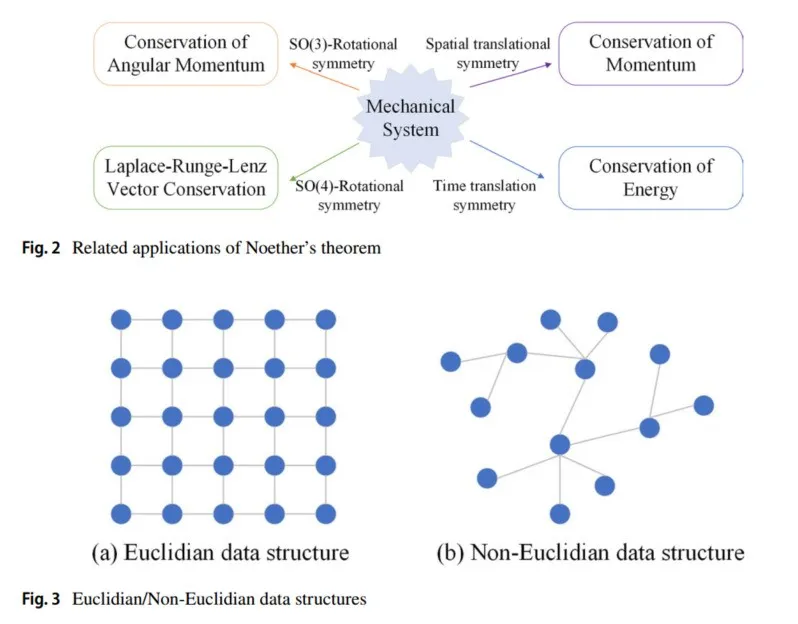
深度学习模拟物理世界的对称性(即物理规律在各种变换下的不变性)。从物理规律的不变性出发,可以得到一个不变量,这被称为守恒量或不变量,宇宙遵循平移/旋转对称性(动量守恒)。动量守恒是空间均匀性(畸变度)的体现,通过数学群论可以解释:空间具有平移对称性——物体经过空间平移变换后,物理运动趋势和相关物理规律保持不变。20世纪,Noether提出了Noether定理,即每一个连续对称性都对应一个守恒定律,相关表达式参见文献(Torres 2003, 2004;Frederico 和 Torres 2007),相关应用见图2。
卷积神经网络(CNN)的平移不变性、局部性和组合性使它们自然适合处理像图像这样的欧几里得结构数据任务。然而,世界上仍然存在复杂的非欧几里得数据,几何深度学习(GDL)应运而生(Gerken等,2023)。从对称性和不变性的角度出发,研究了在非传统平面数据(非欧几里得数据)结构情况下深度学习框架的设计(Michael,2017)。这个术语最早由Michael Bronstein在2016年提出,GDL试图将(结构化的)深度网络推广到非欧几里得领域,如图和流形。数据结构如图3所示。
2.1.1 流形神经网络
流形是具有局部欧几里得空间性质的空间,用于数学中描述几何形状,如雷达扫描返回的各种物体表面的空间坐标。黎曼流形是具有黎曼度量的微分流形,其中黎曼度量是微分几何中的一个概念。简单来说,黎曼流形是一个光滑流形,给定了一个光滑的、对称的、正定的二阶张量场。例如,在物理学中,经典力学的相空间是流形的一个例子,构造广义相对论时空模型的四维伪黎曼流形也是流形的一个实例。
通常,流形数据具有更丰富的空间信息,如球面上的脑磁图(Defferrard等,2020)和人体扫描数据(Armeni等,2017;Bogo等,2014),其中包含局部结构和空间对称性(Meng等,2022)。目前,一种新型流形卷积已被引入物理信息流形中(Masci等,2015;Monti等,2017;Boscaini等,2016;Cohen等,2019;De Haan等,2020),以弥补卷积神经网络不能充分利用空间信息的缺陷。
流形学习是一大类基于流形的框架,恢复低维结构通常被称为流形学习或非线性降维,它是无监督学习的一个实例。流形学习的例子包括:(1)多维标度(MDS)算法Tenenbaum等(2000),该算法侧重于保留高维空间中的“相似性(通常为欧几里得距离)”信息,是另一种线性降维方法;(2)侧重于局部线性嵌入(LLE)算法,降维过程中保留样本的局部线性特征,放弃了所有样本的全局最优降维(Roweis和Saul,2000);(3)t-SNE算法(Maaten和Hinton,2008)使用重尾分布的t分布来避免拥挤问题和优化问题,仅适用于可视化,不能进行特征提取;(4)统一流形近似与投影(UMAP)(McInnes等,2018)算法基于黎曼几何和代数拓扑的理论框架。UMAP与t-SNE一样,仅适用于可视化,UMAP和t-SNE的性能由不同的初始化选择决定(Kobak和Linderman,2019, 2021);(5)谱嵌入,如拉普拉斯特征映射,是一种基于图的降维算法,从局部角度构建数据之间的关系。它希望降维后彼此相关的点(图中连接的点)在空间中尽可能接近,从而在降维后仍能保持原始数据结构(Belkin和Niyogi,2003);(6)扩散映射方法(Wang,2012)使用扩散映射构建数据核,这也是一种非线性降维算法;(7)深度模型(Hadsell等,2006)学习一种模型,可以将数据均匀映射到输出上,得到流形上的全局一致非线性函数(不变映射)进行降维。Cho等(2024)提出了高斯流形变分自编码器(GM-VAE),解决了之前超曲率VAE中常见的局限性。Katsman等(2024)研究了ResNet,并展示了如何以几何学为原则将该结构扩展到一般黎曼流形。
2.1.2 图神经网络
另一种非欧几里得几何数据是图。图是指由节点和边组成的网络结构数据,如社交网络。图神经网络(GNN)的概念最早由Gori等人提出,以扩展现有的神经网络来处理更多类型的图数据(Gori等,2005),然后由Scarselli等(2008)进一步继承和发展。2020年,Wu等(2020)提出了一种新分类方法,为数据挖掘和机器学习领域的图神经网络(GNN)提供了全面概述。Zhou等(2020)提出了GNN模型的一般设计过程,并系统地对应用进行了分类和回顾。在谱图理论背景下首次提出的网络将卷积和池化操作扩展到图结构数据中。输入是图及其上的信号,输出是每个图上的节点(Defferrard等,2016)。
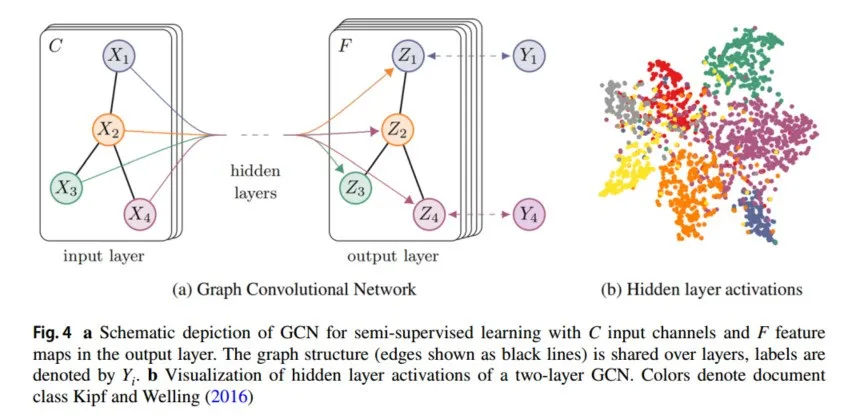
图卷积神经网络(GCN)是GNN的“首创”工作。它采用半监督学习方法来近似原始图卷积操作中的卷积核,并改进了原始图卷积算法(Kipf和Welling,2016),如图4所示。有关GCN在推荐系统中的应用,请参考Monti等(2017)。图卷积网络是许多复杂图神经网络模型的基础,包括基于自编码器的模型、生成模型和时空网络。受物理学启发,Martin等人在2022年《自然机器智能》杂志上发表了一篇文章,使用图神经网络解决组合优化问题(Schuetz等,2022)。为了解决GCN计算量大的局限性,Xu等提出了一种图小波神经网络(GWNN),该网络使用图小波变换来减少计算量(Xu等,2019)。
图注意力网络是一种基于空间的图卷积网络,它结合了自然语言处理中注意力机制与图结构数据的新图几何数据学习。注意力机制用于确定节点邻域的权重,从而产生更有效的特征表示(Velikovi等,2017),适用于(基于图的)归纳学习问题和迁移学习问题。图注意力模型提出了一种递归神经网络模型,可以解决图分类问题。它通过自适应访问每个重要节点的序列来处理图信息。
图自编码器是一类图嵌入方法,旨在使用神经网络结构将图的顶点表示为低维向量。目前,基于GCN的自编码器方法主要包括:GAE(Kipf和Welling,2016)和ARGA(Pan等,2018),以及其他变体如NetRA(Yu等,2018)、DNGR(Cao等,2016)、DRNE(Ke等,2018)。
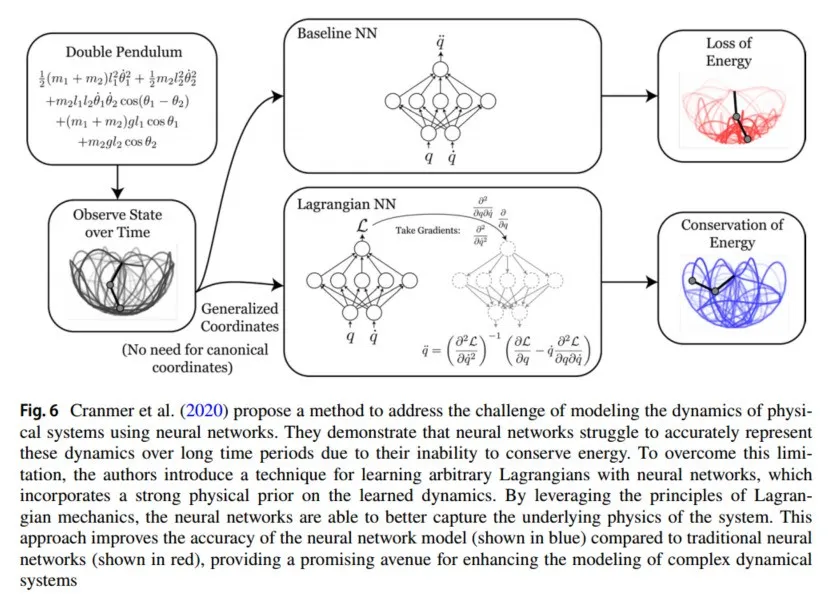
图6 Cranmer 等人 (2020) 提出了一种方法,旨在解决使用神经网络建模物理系统动力学所面临的挑战。他们展示了神经网络由于无法保持能量守恒,因此在长时间段内难以准确表示这些动力学。为克服这一限制,作者提出了一种通过神经网络学习任意拉格朗日量的方法,该方法在所学动力学中引入了强大的物理先验。通过利用拉格朗日力学的原理,神经网络能够更好地捕捉系统的基本物理特性。这种方法提高了神经网络模型(蓝色表示)的准确性,相较于传统神经网络(红色表示)有了显著改进,为增强复杂动力系统建模提供了有前途的方向。
图生成网络的目的是在给定一组观察到的图的情况下生成新图。MolGAN(Lee等,2021)集成了关系GCNs、改进的GANs和强化学习目标,以生成具有模型所需属性的图。DGMG(Li等,2018)利用具有空间特性的图卷积网络来获取现有图的隐藏表示,适用于表达性和灵活的关系数据结构(如自然语言生成、制药领域等)。GRNN(You等,2018)通过两层递归神经网络的深度图生成模型。
除了上述经典模型外,研究人员还对GCN进行了进一步研究。例如,GLCN(Jiang等,2018)、RGDCN(Brockschmidt,2019)、GIC(Jiang等,2019)、HA-GCN(Zhou和Li,2017)、HGCN(Liu等,2019)、BGCN(Zhang等,2018)、SAGNN(Zhang等,2019)、DVNE(Zhu等,2018)、SDNE(Wang等,2016)、GC-MC(Berg等,2017)、ARGA(Pan等,2018)、Graph2Gauss(Bojchevski和Günnemann,2017)和GMNN(Qu等,2019)等网络模型。实际上,DeepMind团队也开始关注图上的深度学习。2019年,Megvii研究院提出了一种用于建模点之间几何结构的GeoConv和一种分层特征提取框架Geo-CNN(Lan等,2019)。Hernández等(2022)提出了一种使用图神经网络预测耗散动力系统时间演化的方法。Yao等(2024)引入了用于半监督节点分类的联邦图卷积网络(FedGCN)算法,该算法具有收敛速度快、通信成本低的特点。
2.1.3 流体动力学神经网络
计算流体动力学(CFD)是现代流体力学结合的产物,其研究内容是通过计算机和数值方法求解流体力学的控制方程,模拟和分析流体力学问题。
Maziar等人提出了科学中的物理神经网络——隐藏流体力学网络框架(HFM),用于求解偏微分方程(Raissi等,2020)。在Raissi等(2020)中,流体的运动由输运方程、动量方程和连续性方程控制,这些方程(流体力学知识)被编码到神经网络中,通过结合神经网络的残差来获得控制方程的可行解,如图5所示。HFM框架不受边界条件和初始条件的限制,实现流体物理数据预测具有机器学习的强大通用性和计算流体动力学的强大针对性的优势。
Wsewles等人提出了NPM–神经粒子法(Wessels等,2020),这是一种使用更新的拉格朗日物理信息神经网络的计算流体动力学方法,即使在离散点位置高度不规则的情况下,NPM也稳定且准确。一种新的端到端学习深度学习神经网络,用于基于拉格朗日流体模拟数据自动生成流体动画(Zhang等,2020)。Guan等提出了“NeuroFluid”模型,该模型使用基于神经隐式场的人工智能可微渲染技术,将流体物理模拟视为求解流体场景三维渲染问题的逆问题,实现了流体动力学反演(Guan等,2022)。
2.2 动态神经网络系统
用于表示非线性函数的方法包括动态系统和神经网络。同时,各种非线性函数实际上是不同层之间传播的信息波。如果将现实世界中的物理系统用神经网络表示,将大大提高将这些物理系统应用于人工智能领域进行分析的可能性。神经网络通常使用大量数据进行训练,并通过获取的大量信息调整数据的权重和偏差。通过最小化实际输出与期望输出值之间的差异,逼近真实值,从而模仿人脑神经元的行为进行判断。然而,这种训练方法存在“混沌盲区”的缺陷,即AI系统无法应对系统中的混沌(或突变)现象。
2.2.1 Hamiltonian/Lagrangian神经网络
瑞士数学家Johann Bernoulli提出的最速降线问题使变分法成为解决数学物理中极值问题的重要工具。物理问题(或其他学科问题)的变分原理通过使用变分方法转化为寻找函数极值(或驻值)的问题。变分原理也称为最小作用量原理(Feynman,2005)。Karl Jacobbit称最小作用量原理为解析力学之母。当应用于机械系统的作用时,可以得到机械系统的运动方程。对该原理的研究促使了经典力学中Lagrangian和Hamiltonian形式的发展。
Hamiltonian神经网络 Hamilton原理是Hamilton于1834年为动态完整系统提出的变分原理。Hamiltonian(动量守恒)体现了一个动态物理系统的完整信息,即存在的所有能量、动能和势能的总量。Hamiltonian原理通常用于建立具有连续质量分布和连续刚度分布的系统(弹性系统)的动态模型。Hamilton是赋予神经网络学习秩序和混沌能力的“特殊调料”。神经网络以传统网络无法理解的方式理解潜在动力学。这是物理学中神经网络的第一步。NAIL团队将Hamiltonian结构融入神经网络,应用于已知的恒星和分子动力学模型Hénon-Heiles模型中,准确预测了系统在秩序和混沌之间的动态变化(Choudhary等,2020)。
一个无结构的神经网络,如多层感知器(MLP),可以用来参数化Hamiltonian。2019年,Greydanus等人提出了Hamiltonian神经网络(HNN)(Greydanus等,2019),该网络学习物理学的基本规律(质量-弹簧系统的Hamiltonian),并准确地保持类似于总能量的量(能量守恒)。同年,Toth等人使用Hamiltonian原理(变分方法)将优化问题转化为函数的极值问题(或驻值),并提出了Hamiltonian生成网络(HGN)(Toth等,2019)。由于Hamiltonian运动方程定义的物理限制,研究Han等(2021)引入了一类可以适应非线性物理系统的HNN。通过训练基于时间序列的神经网络,从目标Hamiltonian系统的一小部分分叉参数值中,预测其他参数值的动态状态。Dierkes和Flaßkamp(2021)的工作引入了Hamiltonian神经网络(HNN),通过训练神经网络学习运动方程,克服了物理规则缺乏的问题,从而显式地学习系统的总能量。
在应用于混沌动态系统的神经网络领域,Haber和Ruthotto(2017)的工作引入了一种称为“稳定神经网络”的神经网络模型,该模型受到Hamiltonian动态系统微分方程的启发。该模型旨在解决通过混沌动态系统离散化获得的神经网络易受输入数据扰动或噪声影响的问题。
另一篇由Massaroli等(2019)撰写的相关研究论文为神经网络优化提供了一种新视角,专门解决逃离鞍点的问题。神经网络训练中的优化问题具有非凸性和高维性,难以收敛到最小损失函数。所提出的框架保证收敛到最小损失函数,并避免鞍点问题。它还展示了其在基于物理系统和pH控制的神经网络中的应用,提高了学习效率,并增加了找到目标函数全局最小值的可能性。
此外,Lin等(2017)的参考文献中讨论了其他识别Hamiltonian动态系统(HDS)的方法,这些方法有助于探索用于建模和理解HDS的神经网络架构和技术。Zhao等(2024)使用保守的Hamiltonian神经流来构建对抗攻击鲁棒的GNN,大大提高了对抗扰动的鲁棒性。
总体而言,这些研究工作强调了将神经网络应用于混沌动态系统的关键方法和视角,解决了输入数据扰动、鞍点问题和优化困难等挑战。
Lagrangian神经网络 解析力学中的Lagrangian函数是描述整个物理系统动态状态的函数。系统的Lagrangian函数表示系统本身的属性。如果世界是对称的(例如空间对称性),则系统在平移后,Lagrangian函数保持不变,并且可以使用变分原理获得动量守恒。
即使训练数据满足所有物理定律,经过训练的人工神经网络仍然可能产生不符合物理规律的预测(在某些情况下,刚体运动学并不适用,甚至难以通过物理公式计算)。因此,2019年在Euler-Lagrangian方程中将物体质量矩阵表示为神经网络,从而可以估计质量分布与机器人姿态之间的关系(Lutter等,2019)。深度Lagrangian网络学习机械系统的运动方程,训练速度比传统前馈神经网络更快,预测结果更符合物理规律,并且在新轨道预测方面更具鲁棒性。
为了增强算法的稀疏性和稳定性,Cranmer等人的工作(2020)提出了一种基于维度约减算法SCAD的稀疏惩罚函数(Fan和Li,2001),并将其添加到Lagrangian约束神经网络中,以克服传统盲源分离方法的缺陷和独立成分分析方法的缺陷,能够有效避免方程的病态问题,提高盲图像恢复的稀疏性、稳定性和准确性。由于神经网络无法保持能量,因此难以在较长时间内对动态建模。2020年,Cranmer等人的研究(2020)使用神经网络学习任意的Lagrangian量,引入了强物理先验,如图6所示。Xiao等(2024)引入了Lagrangian神经网络(LNN)(广义Lagrangian神经网络)的突破性扩展,该扩展创新地为非保守系统量身定制。
2.2.2 神经网络微分方程求解器
在物理学中,由于局部性和因果关系方程的概念,微分方程是基本方程,因此将神经网络视为动态微分方程并使用数值求解算法设计网络结构是一种前沿趋势。
常微分方程神经网络 一般神经ODE如下所示:
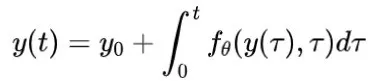
其中
可以是任意维度的张量,
表示学习到的参数向量,
表示神经网络。神经网络提供了强大的函数逼近能力,而惩罚项有助于弥合理论与实践之间的差距。一个应用实例是在湍流建模中,如Ling等(2016)所示,通过精心设计的神经网络逼近闭合关系(Reynolds应力),同时遵守特定的物理不变性。该方法使得理论与观测数据之间的残差建模成为可能。
当结合时间变化组件时,隐式ODEs从该框架中出现。Rubanova等(2019)利用隐式ODEs模拟了小青蛙进入模拟环境中的空气中的动态。此外,Du等(2020)探索了隐式ODEs在强化学习中的应用。
另一个由Shi和Morris(2021)进行的研究将隐式ODEs与变化点检测算法相结合,以模拟切换动态系统。这种方法为分割和理解具有突变的复杂动态提供了强大的工具。
总而言之,结合惩罚项和隐式ODEs的神经网络为建模和模拟各种动态系统(包括湍流、强化学习和切换动态系统)提供了宝贵的方法。这些方法弥合了理论原则与实际应用之间的差距,开启了理解和预测复杂现象的新可能性。

Euler方法:Euler方法的主要思想是使用一个点的一阶导数线性逼近最终值。由于使用一阶导数的位置不同,它分为正向Euler法(也称为显式Euler法)和反向Euler法(隐式Euler法)。深度残差网络(ResNet)(He等,2016)的通用形式可以看作是一个离散动态系统,因为它的每一步都是由最简单的非线性离散动态系统——线性变换和非线性激活函数组成的。可以说,残差网络是神经ODE的显式Euler离散化。现在,RevNet神经网络(Behrmann等,2019)作为ResNet的进一步推广,是具有对称形式的残差学习。反向Euler算法对应于PolyNet(Zhang等,2017),PolyNet通过增加每个残差块的宽度来减少深度,从而实现最先进的分类精度。此外,从常微分方程的角度来看,反向Euler方法比正向Euler方法具有更好的稳定性。有关将常微分方程本身用作神经网络的更多方法,请参见Chen等(2018)。
偏微分方程神经网络 一般形式的二阶偏微分方程:

FractalNet的设计基于自相似性,通过反复应用一个简单的扩展规则生成深度网络,其结构被布置为一个截断的分形Larsson等(2016),其结构可以解释为著名的Runge-Kuta形式。Ramacher(1993)中的神经网络的激活和权重动态是由偏微分方程导出的,并将权重作为参数或变量纳入其中。通过使用参数和动力学的时变模式组合获得的结果表明,在相同性能下,学习规则可以被学习规律所取代。
物理信息神经网络(PINN) Raissi等(2019)是一种将科学计算方法应用于传统数值领域的方法,特别是用于解决与偏微分方程相关的各种问题。PINN的原理是通过训练神经网络来逼近偏微分方程的解,以最小化损失函数。其本质是将方程(物理知识)集成到网络中,并使用控制方程的残差项构建损失函数,该损失函数用作限制可行解空间的惩罚项。
物理信息神经网络(PINN) Raissi等(2019)是一种将科学计算机应用于传统数值领域的方法,特别是用于解决与偏微分方程(PDE)相关的各种问题。PINN的原理是通过训练神经网络以最小化损失函数来逼近PDE的解。其核心思想是将方程(物理知识)集成到网络中,并使用控制方程的残差项构建损失函数,该损失函数作为惩罚项来限制可行解的空间。
PINN-HFM Raissi等(2020)算法融合了物理知识,从稀疏的速度信息中重构了高分辨率的整体速度场。也就是说,最小化NS方程的损失项,同时获得速度场和压力场,使结果符合“物理规律”。与传统的计算流体动力学(CFD)求解器相比,PINN在整合数据(流动的观测)和物理知识(本质上是描述物理现象的控制方程)方面表现得更好。
鉴于PINN在极端梯度下降方面不够稳健,并且深度随着PDE阶数的增加而增加,导致梯度消失和学习率降低,Dwivedi等(2019)提出了DPINN。2020年,Meng等(2020)使用传统的并行时间域分割方法来降低模型的复杂性和学习难度。与PINN及其变体不同,Fang(2021)提出使用微分算子的逼近代替自动微分来求解PDE的混合物理信息网络。Moseley等(2021)的研究提出了一种空间划分区域的并行方法。作为一种无网格方法,PINN不需要网格。因此,Chen等(2021)也提出了一种使用融合微分格式加速信息传播的算法。随后,Schiassi等(2022)利用PINN来解决方程范式问题,用于“学习”平面轨道转移问题的最优控制。自全球爆发Covid-19病毒以来,Treibert等人使用PINN评估了模型参数,建立了SVIHDR微分动力系统模型(Treibert和Ehrhardt,2021),并扩展了易感-感染-康复(SIR)模型(Trejo和Hengartner,2022)。
尽管使用PDE模拟物理问题的AI已经被广泛应用,但在解决高维PDE问题上仍然存在局限性。Karniadakis等(2021)讨论了在满足物理不变性条件下,结合噪声数据和数学模型的物理知识(学科)学习的多种应用,旨在提高精度,解决隐含的物理逆问题和高维问题。Xiao等(2024)提出了一种解决高阶偏微分方程的深度学习框架,名为SHoP。同时,该网络扩展到了泰勒级数,提供了偏微分方程的显式解。
控制微分方程神经网络 神经控制微分方程(CDEs)依赖于两个概念:有界路径和黎曼-斯蒂尔杰斯积分,其形式如下:
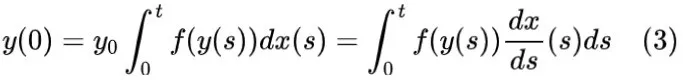
使用神经微分方程对时间序列进行动态建模是一个有前景的选择,然而,当前方法的性能往往受到初始条件选择的限制。由Kidger等人(2020)生成的神经CDE模型可以处理不规则采样和部分观测的输入数据(即时间序列),其性能优于基于常微分方程(ODE)或递归神经网络(RNN)的模型。Morrill等人(2021)在数值求解器中引入了额外的项,以结合子步信息来获得神经粗微分方程。当处理缺失信息的数据时,添加观测掩码已成为一种标准做法,Che等人(2018)提出了这一做法,这是适当的连续时间类比方法。
随机微分方程神经网络 随机微分方程(SDE)在建模真实世界的随机现象中得到了广泛应用,如粒子系统(Coffey 和 Kalmykov 2012;Pavliotis 2014)、金融市场(Black 和 Scholes 2019)、人口动态(Arató 2003)和遗传学(Huillet 2007)。隐式ODEs作为常微分方程(ODEs)的自然扩展,用于建模在连续时间内演化的系统,同时考虑到不确定性(Kidger 2022)。
随机微分方程(SDE)的动力学包含一个确定性项和一个随机性项:
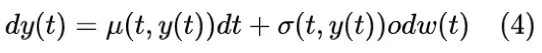
其中,
和
是正则函数,
是一个
维的布朗运动,
是结果的
维连续随机过程。
随机微分方程(SDE)中固有的随机性可以被视为现代机器学习背景下的生成模型。类似于递归神经网络(RNNs),SDEs 可以被看作是带有随机噪声的RNN,特别是布朗运动作为输入,生成的样本作为输出。时间序列模型是经典的兴趣模型。预测模型如Holt-Winters(Holt 2004)、ARCH(Engle 1982)、ARMA(Hannan 和 Rissanen 1982)、GARCH(Bollerslev 1986)等。
更多用于解决微分方程并结合物理知识和机器学习的深度学习库可以参考Lu等人的文献(2021)。
2.3 使用图神经网络解决物理问题
分子设计:材料和制药领域中最关键的问题是从分子结构预测新分子的化学、物理和生物特性。哈佛大学的Duvenaud等人(2015)最近的研究提出将分子建模为图结构,并使用图卷积神经网络(GCN)来学习所需的分子特性。他们的方法显著优于Morgan(1965)、Rogers和Hahn(2010)手工设计的能力,这一工作为以新方式进行分子设计打开了机会。
医学物理:医学物理是人工智能应用的最重要领域之一,可以大致分为放射治疗和医学影像。随着AI在成像任务中的成功,AI在放射治疗(Hrinivich和Lee,2020;Maffei等,2021)和医学影像(如X光、MRI和核医学)(Barragán-Montero等,2021)中的研究迅速增长。其中,磁共振成像(MRI)技术在医学图像分析中的应用(Castiglioni等,2021)在许多疾病的诊断、管理和监测中起着至关重要的作用(Li等,2022)。帝国理工学院的一项最新研究(Ktena等,2017)使用图CNN对非欧几里得脑成像数据进行处理,以检测自闭症相关的大脑功能网络中的紊乱。Zegers等人概述了神经肿瘤学MRI中深度学习的最新应用状态(Zegers等,2021),这具有广泛的潜在应用。Rizk等人在经过外部验证后引入了用于半月板撕裂检测的深度学习模型(Rizk等,2021)。MRI图像重建工作的讨论和总结(Montalt-Tordera等,2021)为未来临床数据对的获取提供了巨大潜力。
高能物理实验:引入图神经网络来预测N体系统的动力学(Battaglia等,2016;Chang等,2016),并取得了显著的成果。
电力系统求解器:Donon等人的研究(2019)结合了图神经网络,提出了一种用于解决电力微分方程的神经网络架构,以计算电网中的功率流动(所谓的“负载流”)。Park和Park的工作(2019)提出了一种用于风电场功率估算任务的物理启发数据驱动模型。
玻璃系统的结构预测(玻璃相变):DeepMind在《Nature Physics》上发表了一篇论文(Bapst等,2020),利用图神经网络模型对玻璃动力学进行建模,将网络预测与物理学联系起来。仅使用隐藏在粒子周围的结构就可以预测玻璃系统的长期演化。该模型在不同的温度、压力和密度范围内表现良好,展示了图网络的强大能力。
3 由电磁学启发的深度神经网络范式
3.1 光学设计神经网络
光学神经网络(ONNs)是一种利用光学技术(如光学连接技术、光学器件技术等)设计的新型神经网络。光学神经网络的理念是通过利用调制将信息附加到光学特性上来模仿神经网络。同时,利用光的传播原理,如干涉、衍射、透射和反射,实现神经网络及其操作符。ONNs的首次实现是光学Hopfield网络,由Demetri Psaltis和Farhat于1985年提出。在传统神经网络中主要涉及三个操作符:线性操作、非线性激活操作和卷积操作,本节将依次介绍上述操作符的光学实现。我们在表2中总结了本节的结构和代表性方法的概述。
3.1.1 线性操作的光学实现
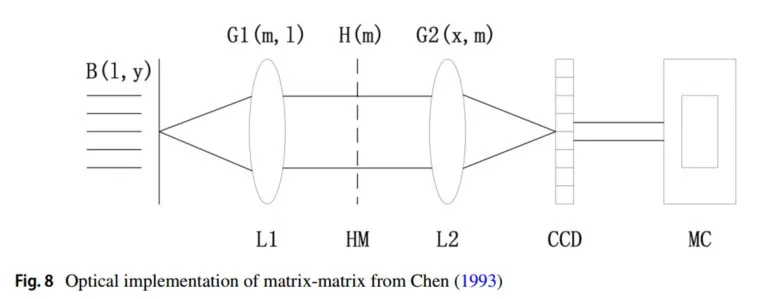
神经网络的主要线性操作符是矩阵乘法操作符和加权求和操作符。由于光的相干性和非相干性的特性,加权求和操作符较容易实现,因此线性操作的光学实现挑战在于矩阵乘法的光学实现。早在1978年,J. W. Goodman等(1978)就根据光学传输原理,利用透镜组首次实现了光学向量-矩阵乘法器;矩阵-矩阵乘法器的光学实现则首次由Chen(1993)使用由透镜组组成的4f型系统实现。
向量-矩阵乘法的光学实现 向量
是通过将矩阵
与向量
相乘得到的。其数学本质是利用矩阵
的每一行与向量
进行内积,从而获得对应位置的向量
的值。数学表达式为:
光学向量-矩阵乘法器主要由两部分组成:光源部分,如发光二极管光源阵列,以及由球面透镜、柱面透镜、空间光调制器(SLM)和光学检测器组成的光路系统。其数学思想是将向量-矩阵乘法转化为矩阵-矩阵逐点乘法。
如图7所示,向量
被调制到非相干光源(LS)的光学特性上,如振幅、强度、相位和偏振态。然后,入射光通过第一个球面透镜L1。由于LS阵列位于球面透镜L1的前焦平面上,光通过L1后以平行形式发射。接下来,光通过柱面透镜CL1,CL1位于L1的后焦平面上。由于CL1的垂直放置,通过CL1的光仅在水平方向上聚集,而在垂直方向上平行发射,此时光场携带的信息为:
在CL1的后焦平面上放置了一个空间光调制器(SLM),其中包含了矩阵
的信息。光通过SLM的过程可以视为矩阵
和
的点乘过程。在此时,光场携带的信息为:
然后,光通过CL2柱面透镜,CL2与SLM之间的距离为CL2的焦距
。由于CL2的水平放置,通过SLM的光仅在垂直方向上聚集,而在水平方向上平行发射。在此时,光场携带的信息为向量
的乘积结果:
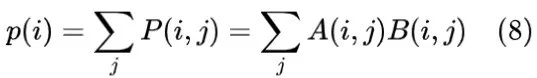
最后,光通过CL2被解调,并且可以使用电荷耦合器件(CCD)获得向量
。
矩阵-矩阵乘法的光学实现
相比于向量-矩阵乘法,矩阵-矩阵乘法更为复杂。矩阵
和矩阵
的乘积是矩阵
的每一行与矩阵
的每一列的内积。假设结果矩阵为
,其表达式如下:
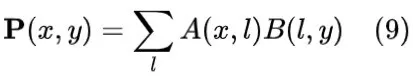
矩阵-矩阵乘法的实现依赖于光学4f型系统,该系统由傅里叶透镜、全息掩膜(HM)和电荷耦合器件组成。利用离散傅里叶变换(DFT),可以使用离散傅里叶变换矩阵构造矩阵
来实现乘法。
如图8所示,矩阵
在输入光的复振幅上被调制,结果矩阵
在输出平面上获得。矩阵
和
的乘法操作是在光从输入平面传播到输出平面的过程中完成的。设矩阵
和函数
为输入光场,傅里叶透镜前焦平面的傅里叶变换函数分别表示为:
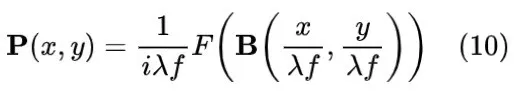
由于DFT可以通过DFT矩阵实现,结合公式(10),离散光场的表达式为:
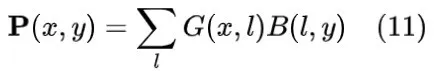
在这种情况下,透镜的DFT矩阵
仅与焦距和波长相关,因此矩阵
必须通过全息掩膜进行调制,用于调整光场的复振幅分布。整个光学系统由两个傅里叶透镜和一个全息掩膜组成,因此输出光场为:
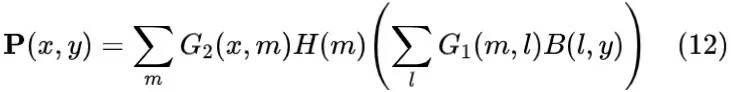
其中,矩阵
和
分别表示两个透镜的DFT矩阵,而
是全息掩膜的复振幅分布函数。对比公式(9)和公式(12):
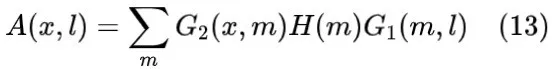
输入平面、输出平面和全息掩膜的采样周期与采样数之间的关系满足:
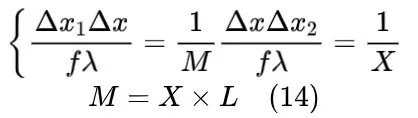
其中,
,
,
,
,
,
是分别表示输入平面、全息掩膜和平面的采样周期和采样数。根据公式(13)和公式(14),可以得到
:
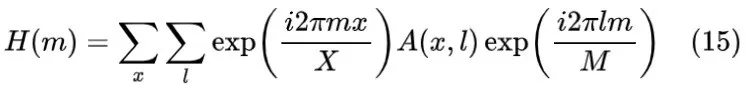
光学矩阵乘法器 向量-矩阵乘法器最早由J. W. Goodman等人于1978年提出。通过该乘法器,离散傅里叶变换(DFT)以光学方式实现。这些研究(Liu等,1986;Francis等,1990;Yang等,1990)提出使用微型液晶电视(LCTV)构建空间光调制器,以替代矩阵掩膜和透镜实现矩阵乘法。Francis等(1991)的研究提出使用镜面阵列代替常用的透镜阵列来实现使用镜面阵列互连的光学神经网络;Nitta等(1993)的研究去掉了矩阵乘法器中的两个柱面透镜,改进了发光二极管阵列和可变灵敏度光电探测器阵列,并生产了第一个光学神经芯片。Chen(1993)的研究提出构建光学4f型系统,利用傅里叶透镜的光学傅里叶变换和反变换实现矩阵-矩阵乘法。Wang等(1997)的研究提出了一种新的光学神经网络架构,该架构使用两个垂直的一维棱镜阵列进行光学互连,以实现矩阵乘法。
Psaltis等(1988)提出了使用光折变晶体的动态全息修改来实现矩阵乘法,从而能够构建大多数神经网络。Slinger(1991)提出了一种加权N对N体积全息神经互连方法,并推导出了描述理想化互连行为的耦合波解。(Yang等,1994;Di Leonardo等,2007;Nogrette等,2014)提出使用Gerchberg-Saxton算法计算每个区域的全息图。Lin等(2018)的研究提出使用透射和反射层形成纯相位掩膜,并通过光衍射构建全光学神经元。Yan等(2019)提出了一种新型的衍射神经网络,通过在光学系统的傅里叶平面上放置衍射调制层来实现。Qian等(2020)的研究提出在化合物惠更斯超表面上以衍射方式散射或聚焦微波频率的平面波,以模拟人工神经网络的功能。
Lin等,Mengu等(2019)提出使用五个纯相位衍射层进行复数相位调制和复数振幅调制,以实现光学衍射神经网络。Shen等(2017),Bagherian等(2018)利用马赫-曾德尔干涉仪阵列通过奇异值分解原理实现矩阵乘法;Hamerly等(2019)提出了一种基于光干涉的零差检测方法来实现矩阵乘法,并构建了一种新型光子加速器以实现光学神经网络。Zang等(2019)通过拉伸时域脉冲实现了向量-矩阵乘法。在光纤环的帮助下,可以在光学中实现多层神经网络。
3.1.2 非线性激活的光学实现
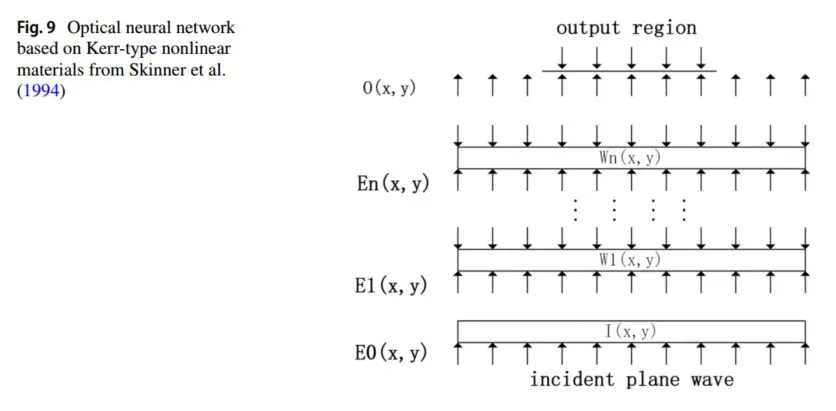
非线性激活函数在神经网络中起着重要作用,使其能够逼近复杂的非线性映射。然而,由于光学中缺乏非线性响应以及光学器件制造条件的限制,器件的光学响应通常是固定的,这限制了光学非线性无法重新编程以实现不同形式的非线性激活函数。因此,之前在光学神经网络(ONNs)中的非线性通常是通过光电混合方法实现的(Dunning等,1991)。随着材料制造条件的发展,全光学非线性的实现(Skinner等,1994)才开始出现。以下将以一个示例进行展示(图9)。
全光神经网络由线性层和非线性层组成,线性层由厚的线性介质(如自由空间)构成,而非线性层由薄的非线性介质(如Kerr型非线性材料)构成。这种非线性材料的折射率满足以下关系式:
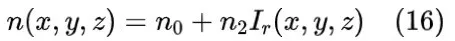
其中,
是线性折射率成分,
是非线性折射率系数,
是光场强度。如果
,材料表现为自聚焦;如果
,材料表现为自散射。由于其折射率依赖于光强度,非线性层可以同时起到加权求和和非线性映射的作用。
当输入光照射到非线性层的平面时,不同点的折射率会有所不同,这会导致透射光的强度和方向发生变化,并出现干涉现象,因此非线性层实现了空间光调制的功能。最终的输出光信号取决于第一层的输入以及非线性层的连续加权与非线性映射。
光电混合方法
Dunning等人(1991)通过帧抓取器和图像处理器逐点处理视频信号,实现了可编程的非线性激活函数。Larger等人(2012)使用集成的电信Mach-Zehnder调制器提供电光非线性调制传递函数,以实现光学神经网络的构建。Antonik等人(2019)通过空间光调制器调制空间扩展平面波的相位,以提高光学系统的并行性,从而显著提高了网络的可扩展性和处理速度。Katumba等人(2019)利用电光探测器的非线性构建网络的非线性算子,实现了极高的数据调制速度和大规模网络参数更新。Williamson等人(2019)和Fard等人(2020)将一小部分入射光转换为电信号,并借助电光调制器对原始光信号进行调制,实现了神经网络的非线性,从而增加了系统的工作带宽和计算速度。
全光方法
Skinner等人(1994)利用Kerr型非线性光学材料作为分隔自由空间的薄层,实现了加权连接和非线性映射,从而提高了光学神经网络的响应速度。Saxena和Fiesler(1995)使用液晶光阀(LCLV)实现了非线性函数的阈值效应,并构建了光学神经网络,以避免光电转换中的能量损失问题。Vandoorne等人(2008,2014)使用耦合半导体光放大器(SOA)作为基本模块,实现全光神经网络中的非线性,使得网络具有低功耗、高速度和高并行性。Rosenbluth等人(2009)使用新型非线性光纤作为阈值,以在网络中实现非线性响应,克服了数字光学计算中的标量问题和模拟光学计算中的噪声累积问题。Mesaritakis等人(2013),Denis-Le Coarer等人(2018),Feldmann等人(2019)利用环形谐振器的非线性折射率变化特性,提供网络的非线性响应,使光学神经网络具有高集成度和低功耗。Lin等人(2018)提出了一种仅使用光衍射和被动光学元件协同工作的光学神经网络方法,避免了功率层的使用,并建立了一种高效快速的机器学习任务实现方式。Bao等人(2011);Shen等人(2017);Schirmer和Gaeta(1997)利用纳米光子的可饱和吸收特性在网络中实现非线性。Miscuglio等人(2018)讨论了通过反向可饱和吸收特性和纳米光子的电磁感应透明性在全光神经网络中实现非线性的方法。Zuo等人(2019)使用空间光调制器和傅里叶透镜来编程线性操作,并通过激光冷却原子的电磁感应透明性实现非线性光学激活函数。
3.1.3 卷积神经网络的光学实现
通过模拟生物视觉的信息分层处理机制,卷积神经网络(CNN)具有局部感知和权重共享的特性,显著降低了计算复杂度,使网络具有更强的拟合能力,能够拟合更复杂的非线性函数。
Shan等人(2018)提出了一种深度卷积神经网络,以加速电磁模拟,并通过强大的非线性函数逼近能力预测静电势分布的三维泊松方程。Li等人(2018)提出了一种称为DeepNIS的新型深度神经网络架构,用于非线性逆散射问题(ISPs)。DeepNIS由多层复值残差CNN级联组成,以模拟多散射机制。该网络将接收器收集的电磁散射数据作为输入,并输出超分辨率的电磁逆散射图像,将粗略的图像映射到ISPs的精确解。Wei和Chen(2019)提出了一种基于物理启发的感应电流学习方法(ICLM),用于解决全波非线性ISPs。该方法设计了一种新颖的CEE-CNN卷积网络,通过跳跃连接将大部分感应电流直接馈送到输出层,并关注其他感应电流。该网络定义了多标签组合损失函数,以减少目标函数的非线性,加速收敛。Guo等人(2021)提出了一种复值Pix2pix生成对抗网络。该网络由两部分组成:生成器和判别器。生成器由多层复值CNN组成,判别器计算原始值与重构值之间的最大似然性。通过判别器和生成器之间的对抗训练,生成器可以捕捉比传统CNN更多的非线性特征。Tsakyridis等人的工作(2024)概述并讨论了光子神经网络和光学深度学习的基本原理。Matuszewski等人(2024)讨论了全光神经网络的作用。
4 深度神经网络范式受统计物理学启发
人工智能领域包含了广泛的算法和建模工具,能够处理各个领域的任务,并已成为近年来最热门的课题。在前面的章节中,我们回顾了人工智能与经典力学和电磁学交叉领域的最新研究。这些研究包括基于物理学洞察力的人工智能概念发展、人工智能技术在多个物理学领域的应用以及这两个领域之间的交叉点。接下来,我们将描述如何使用统计物理学来理解AI算法,以及AI如何应用于统计物理学领域。表3中展示了代表性方法的概述。
4.1 非平衡神经网络
非平衡统计物理学中最普遍的问题是对物理(化学或天文学)系统时间演化的详细描述。例如,趋向于平衡状态的不同现象,考虑系统对外部影响的响应、由波动引起的亚稳态和不稳定性、模式形成和自组织、违背确定性描述的概率的出现、开放系统等。非平衡统计物理学创造了不仅与物理学相关的概念和模型,还与信息、技术、生物学、医学和社会科学密切相关,甚至对基本的哲学问题产生了重大影响。
4.1.1 从熵理解神经网络
熵 由德国物理学家克劳修斯于1865年提出,是热力学发展的一个基本概念。其本质是系统的“固有混乱程度”,或者系统中的信息量(系统越混乱,信息量越少,越难以预测,信息熵越大),在公式中用
表示。它总结了宇宙的基本发展规律:宇宙中的事物有自发变得更加混乱的趋势,这意味着熵将持续增加,这就是熵增原理。
玻尔兹曼分布 1877年,玻尔兹曼提出了熵的物理解释:系统的宏观物理性质可以看作是所有可能微观状态的等概率统计平均。
信息熵(学习成本) 直到统计物理和信息理论的发展,香农在1948年将统计物理中的熵概念扩展到通信过程,并提出了信息熵,熵的普遍意义变得更加明显。
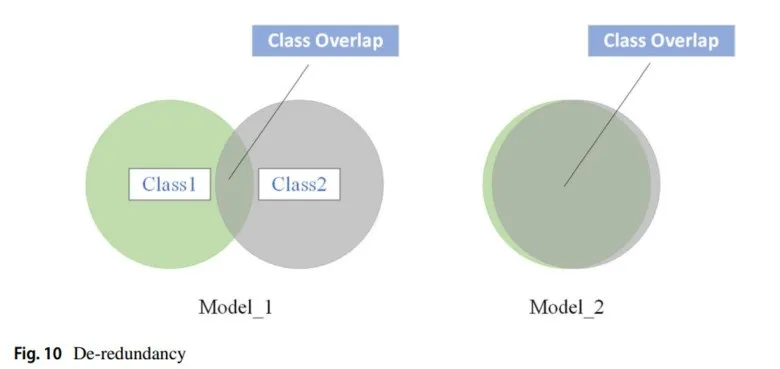
在深度学习中,模型接收信息的速度是固定的,因此加快学习进度的唯一方法是减少学习目标中的冗余信息。所谓的“去粗取精”就是深度学习模型中的最小熵原理,可以理解为“减少不必要的学习成本”(见图10)。
最小熵原理启发的算法应用包括使用信息熵表示最短代码长度的InfoMap(Rosvall等人,2009;Rosvall和Bergstrom,2008)、成本最小化(Kuhn,1955;Riesen和Bunke,2009)、Word2Vec(Mikolov等人,2013a,b)、t-SNE降维(Maaten和Hinton,2008)等。
4.1.2 混沌神经网络
混沌指的是确定性动态系统由于对初始值的敏感性而表现出的不可预测的、类似随机的运动。Poole等人(2016)在NIPS上发表的一篇文章将黎曼几何和动态平均场理论结合,通过随机深度网络的传播分析信号,并在相平面中形成方差权重和偏差。该研究揭示了信号传播在有序状态和混沌状态之间的动态相变。Lin和Chen(2009)提出了一种基于正弦激活函数的混沌动态神经网络,该模型与其他模型不同,具有强大的记忆存储和检索能力。Keup等人(2021)在2020年版的论文中开发了一种用于随机网络的统计平均场理论,以解决瞬态混沌问题。
4.1.3 从伊辛模型到霍普菲尔德网络
在日常生活中,我们看到的相变无处不在,表现为从一种相变到另一种相。例如:液态水冷却形成冰,或加热蒸发成水蒸气(液相到固相,液相到气相)。根据朗道的理论,相变过程必须伴随着某种“有序性”变化。例如,液态水分子是无序排列的,一旦冻结,它们就会在规则有序的晶格位置排列(分子在晶格位置附近振动,但不会远离),因此水结冰。晶体的有序性是在液-固相变过程中产生的,如图11所示。
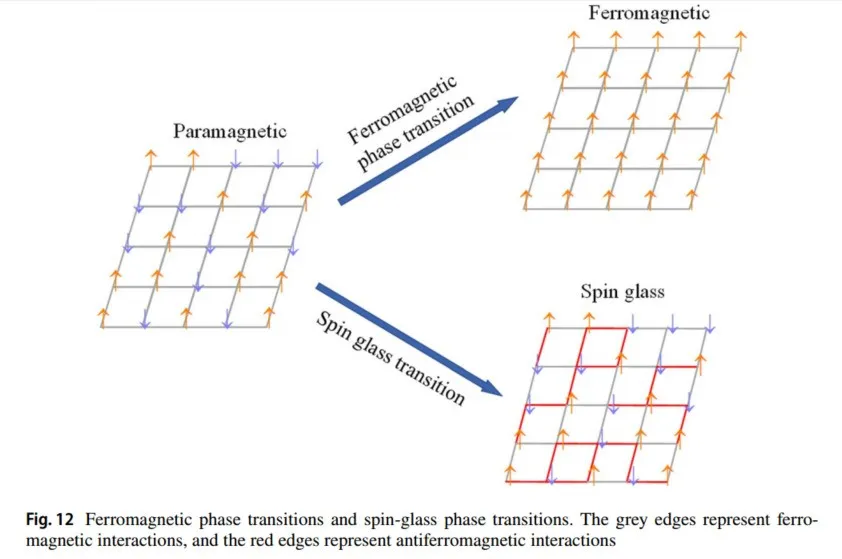
另一个重要的相变例子是铁磁相变:加热过程中,磁铁(铁磁相)失去磁性,变为顺磁相。在铁磁相变过程中(如图12所示),原子的自旋方向从顺磁相中的随机状态变为特定方向,因此铁磁相变伴随着自旋方向顺序的产生,导致材料的宏观磁性(自发磁化)。根据朗道的理论,序参量在连续/不连续相变中分别发生连续/不连续变化。
恰好在100年前,解决相变问题的数学关键出现了,即自旋玻璃模型的“初版”——伊辛模型(相变的基本模型)。伊辛模型(也称为Lenz-Ising模型)是统计物理中最重要的模型之一。在1920年至1924年间,威廉·伦茨和恩斯特·伊辛提出了一类描述物质相变随机过程的伊辛模型。以二维伊辛晶格模型为例,任意点
的状态可以有两个值
(自旋向上或向下),仅受其相邻点的影响(相互作用强度
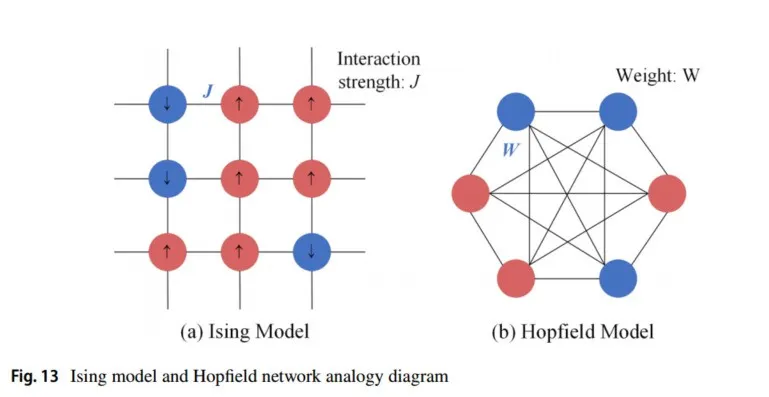
),系统的能量可以通过以下方式获得(哈密顿量):对于伊辛模型,如果所有自旋方向一致,系统的哈密顿量处于最低值,系统处于铁磁相。同样,热力学第二定律告诉我们,在给定温度和熵的情况下,系统会寻求一种能量最小化的配置方法,使用吉布斯-博戈柳博夫-费曼不等式对伊辛模型进行变分推理以获得最优解。1982年,霍普菲尔德受伊辛模型的启发,提出了一种霍普菲尔德神经网络(Hopfield,1982),可以解决大类模式识别问题,并给出一类组合优化问题的近似解。其权重模拟了伊辛模型中相邻自旋的相干性;神经元更新模拟了伊辛模型中的细胞更新。霍普菲尔德网络的单元(全连接)是二进制的,接受值为-1或1,或0或1;它还提供了一个模拟人类记忆的模型(伊辛模型和霍普菲尔德网络的类比图如图13所示)。
霍普菲尔德以能量函数的思想形成了一种新的计算方法,并明确了神经网络与动力学的关系。他利用非线性动力学方法研究了该神经网络的特性,并建立了神经网络的稳定性判据。同时,他指出信息是存储在网络各神经元之间的连接上,形成了所谓的霍普菲尔德网络。通过将反馈网络与统计物理中的伊辛模型进行比较,将磁自旋的上下方向视为神经元激活和抑制的两种状态,将磁自旋的相互作用视为神经元的突触权值。这种类比为大量物理理论和许多物理学家进入神经网络领域铺平了道路。1984年,霍普菲尔德设计并开发了霍普菲尔德网络模型的电路,指出神经元可以用运算放大器实现,所有神经元的连接可以通过电子电路模拟,这就是所谓的连续霍普菲尔德网络。利用这一电路,霍普菲尔德成功地解决了旅行商(TSP)计算难题(优化问题)。
Liu等人(2019)讨论了一种基于霍普菲尔德混沌神经网络的图像加密算法。该算法利用神经网络的迭代过程同时对彩色图像进行扰乱和扩散,修改像素值。加密过程生成高度随机化和复杂的加密图像。在解密过程中,原始图像通过霍普菲尔德神经网络的迭代过程逆转而恢复。
2023年,Lin等人(2023)回顾了基于记忆阻抗霍普菲尔德神经网络的混沌系统研究。该研究探讨了使用这些神经网络构建混沌系统的方法,这些神经网络结合了记忆阻抗以保留电阻变化。文章讨论了通过调整网络参数和连接权值实现的混沌系统的特性和应用。这些研究为理解和应用图像加密和混沌系统提供了新的思路和方法。Ma等人(2024)提出了一种具有消息传递机制的变分自回归架构,可以有效利用自旋变量之间的相互作用。Laydevant等人(2024)通过平衡传播算法以监督方式训练伊辛机,这有可能增强机器学习的应用。
4.1.4 经典模拟退火算法
物理退火过程:首先,物体处于无定形状态,然后将固体加热到足够高的水平以使其变得无序,然后慢慢冷却,退火为晶体(平衡状态)。
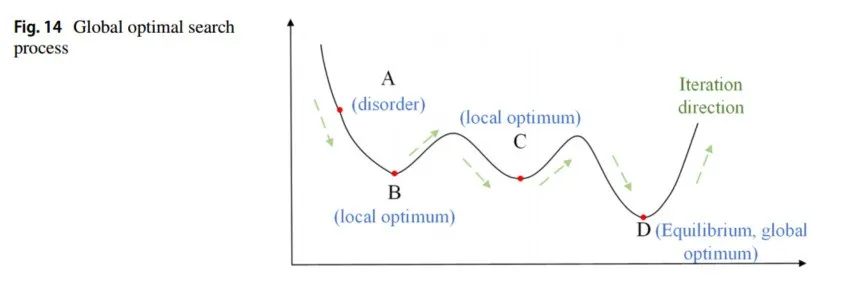
模拟退火算法最早由Metropolis等人在1983年提出,Kirkpatrick等人在1983年将其应用于组合优化,形成了经典的模拟退火算法:利用物理中固体物质的退火过程与一般优化问题之间的相似性;从某一初始温度开始,随着温度的不断下降,结合Metropolis准则的概率突变特性(以一定概率接受新状态),在解空间中搜索,并以概率1停留在最优解上(图14)。
重要抽样(IS)是一种有效的减少罕见事件方差的算法,如Marshall(1954)的开创性工作中所述。IS的基本概念涉及通过从更简单的分布函数中随机加权平均来近似计算,代表目标函数的数学期望。
受到退火思想的启发,Radford提出了退火重要抽样(AIS)作为解决与IS相关的高偏差问题的解决方案。AIS及其扩展版哈密顿退火重要抽样(HAIS)是IS的广义形式,通过重新加权来自可处理分布的样本来计算无偏期望。
在AIS中,构建了一个连接正向和反向马尔可夫链的桥梁,将感兴趣的两个分布连接起来。该桥梁允许与单独使用IS相比,估计方差更低。通过利用正向和反向链之间的连接,AIS在估计罕见事件的期望方面提供了更高的准确性和效率。总之,重要抽样(IS)是一种用于罕见事件的方差减少算法,而退火重要抽样(AIS)及其扩展版HAIS提供了解决与IS相关的偏差问题的解决方案。AIS构建了连接正向和反向马尔可夫链的桥梁,允许比单独使用IS实现更低方差的估计。这些技术在涉及罕见事件的复杂问题的期望估计中提供了更高的准确性和效率。
后来,Ranzato的MCRBM模型(2010),Dickstein的非平衡扩散模型(2015)和Menick的自缩放像素网络自回归模型(2016)相继出现。为了使网络空模型适应加权网络推理,Milisav等人(2024)提出了一种模拟退火过程,以生成具有强度序列保留的随机网络。模拟退火算法应用广泛,可以有效解决NP完全问题,如旅行商问题、最大切割问题、01背包问题、图着色问题等。
4.1.5 玻尔兹曼机神经网络
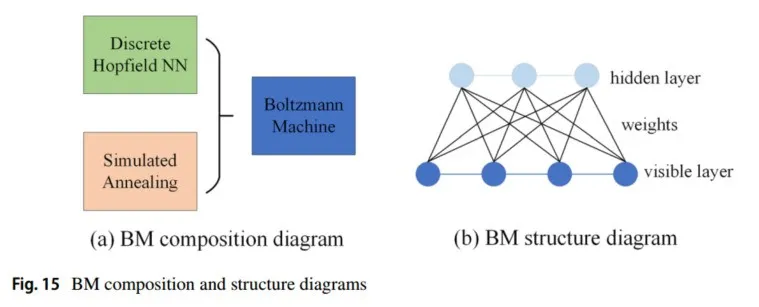
Hinton于1985年提出了玻尔兹曼机(BM),在物理学中通常称为反伊辛模型。BM是一种特殊形式的对数线性马尔可夫随机场(MRF),即能量函数是自由变量的线性函数。它在神经元状态变化中引入了统计概率,网络的平衡状态服从玻尔兹曼分布,网络的操作机制基于模拟退火算法(如图15所示),这是一种良好的全局最优搜索方法,并广泛应用于一定范围内。有关玻尔兹曼机的最新研究,参见Nguyen等人(2017)。
受限玻尔兹曼机(RBM)是玻尔兹曼机(BM)的一种类型,表现出其神经元之间的特定结构和相互作用模式。在RBM中,显层神经元和隐层神经元是通过高效耦合相互作用的两个变量。与一般BM不同,在BM中,所有神经元都可以相互作用,而在RBM中,交互作用仅在显单元和隐单元之间发生。
RBM的目标是通过调整其参数,使观察到的数据的似然性最大化。通过学习显单元和隐单元之间连接的权重和偏差,RBM旨在捕捉和表示数据中存在的潜在模式和依赖性。通过迭代学习过程,RBM调整其参数,以提高生成观察数据的可能性,从而增强其建模和生成类似数据实例的能力。
关于RBM,物理学中有许多研究揭示了它们的工作原理以及可以学习到的结构。自从Hinton教授提出RBM的快速学习算法对比散度以来,为了增强RBM的表达能力并考虑数据的特定结构,已经提出了许多RBM的变体模型(Bengio 2009;Ranzato等,2010;Ranzato和Hinton,2010)。卷积受限玻尔兹曼机(CRBM)是RBM模型中的一项新突破。它使用滤波器和图像卷积操作来共享权重特征,以减少模型的参数。由于RBM学习的大多数隐单元状态未被激活(非稀疏),研究人员结合稀疏编码的想法,在原始RBM的对数似然函数中添加了稀疏惩罚项,并提出了稀疏RBM模型(Lee等人,2007),稀疏群受限玻尔兹曼机(SGRBM)模型(Salakhutdinov等人,2007)和LogSumRBM模型(Ji等人,2014)等。在文章(Cocco等人,2018;Tubiana和Monasson,2017)中,作者研究了具有随机、稀疏和未学习权重的随机受限玻尔兹曼机(RBM)模型。令人惊讶的是,他们发现即使是单层RBM也可以通过隐藏层捕捉组合结构。这突出了RBM在表示复杂数据方面的表达能力。
此外,还探讨了具有随机权重的RBM与霍普菲尔德模型之间的关系(Barra等,2018;Mézard,2017)。这些研究展示了RBM与霍普菲尔德模型之间的联系和相似之处,揭示了两种模型的基本机制和特性。
总的来说,这些工作为具有随机权重的RBM在捕捉组合结构方面的能力以及它们与霍普菲尔德模型的联系提供了见解。这类研究增强了我们对RBM的理解及其在各个领域的潜在应用。
4.2 能量模型设计神经网络
根据物理学知识,事物的稳态实际上代表了其对应的最低势能状态。因此,事物的稳态对应于某种能量的最低状态,并被移植到网络中,从而构建了网络处于稳态时的能量函数定义。
在2006年,LeCun等人回顾了基于能量模型的神经网络及其应用。当模型达到最优解时,它处于最低能量状态(即,它寻求将正向数据的能量最小化,并将负向数据的能量最大化)【LeCun et al., 2006】。任务是找到那些给定观测变量的隐藏变量配置,使能量值最小化(推理);并找到一个合适的能量函数,使观测变量的能量低于隐藏变量的能量(学习)。
在高维空间中,归一化概率分布的实现变得困难,这导致了一种有趣的数据生成建模方法【Pernkopf et al., 2014】。当进行归一化时,虽然可以通过分析来完成,但这些有趣的方法仍可以在参考文献【Wang, 2018】中找到。
4.2.1 生成对抗网络(GANs)
在2014年,Goodfellow等人提出了GAN【Goodfellow et al., 2014】,其目的是生成与训练集类型相同的样本,实质上是使用学习到的判别器判断来替代显式概率评估,可以利用监督学习过程中获取的知识进行无监督学习。基于物理启发的GAN研究开始出现,例如,Wang等人【2019】在GAN的可解释模型中使用早期在线学习的统计物理工作来推广感知器。
深度卷积生成对抗网络(DCGAN)【Radford et al., 2015】的判别器和生成器都使用CNN来替代GAN中的多层感知器,能够将监督学习和无监督学习结合在一起。CycleGAN【Zhu et al., 2017】可以在源域和目标域之间实现模式转换,而无需建立训练数据之间的一对一映射。GCGAN【Fu et al., 2019】是在原始GAN上增加卷积约束,能够稳定学习配置。WGAN【Arjovsky et al., 2017】改进了基于GAN的损失函数,并在全连接层上也能获得良好的性能结果。
4.2.2 变分自编码器模型(VAEs)
自编码器(AE)是一种前馈神经网络,旨在找到数据的简洁表示,同时仍然保持每个样本的显著特征,具有线性激活的自编码器与PCA密切相关。VAE【Kingma and Welling, 2013】结合了变分推理和自编码器,用于模拟能量分布函数之间的转化——构建生成对抗网络为数据提供了一个深度生成模型,从潜在变量Z生成目标数据X,可以在无监督的情况下进行训练。VAE模型更接近物理学家的思维方式,其中自编码器通过图形模型表示,并使用潜在变量和变分先验进行训练推理【Cinelli et al., 2021; Vahdat and Kautz, 2020】。Rezende等人【2014】的研究是理解VAE的基础版本。
一种有趣的生成建模方法涉及将概率分布分解为自回归模型中的一维条件分布的乘积,正如Van Oord等人的工作【2016】中所讨论的那样。这种分解允许通过逐次生成每一维度并基于前一维度进行条件生成,来高效地建模复杂的高维数据,例如图像。
在变分自编码器(VAEs)的背景下,另一种有趣的方法是用可处理的变分近似来替代后验分布。这一想法在Kingma和Welling【2013】、Gregor等人【2014】以及Rezende等人的开创性工作中提出。通过引入一个将输入数据映射到潜在空间的编码器网络和一个从潜在空间重建数据的解码器网络,VAEs实现了高效且可扩展的生成建模。
这些技术,即在自回归模型中分解概率分布并在VAEs中使用可处理的变分近似,为生成建模提供了有趣且有效的策略。它们为复杂数据分布建模提供了见解,并在图像生成和数据合成等多个领域中得到了应用。
4.2.3 自回归生成模型
自回归生成模型【Van Oord et al., 2016; Salimans et al., 2017】是一种可控的建模分布的方法,允许最大似然训练而无需潜在随机变量,其中条件概率分布由神经网络表示。由于这种模型是显示概率的一个家族,可以进行直接且无偏的采样。这些模型的应用已在统计学【Wu et al., 2019】和量子物理问题【Sharir et al., 2020】中得以实现。
神经自回归分布估计(NADE)是一种基于自回归模型和前馈神经网络的无监督神经网络【Zhang et al., 2019】,它是用于建模数据分布和密度的可处理且高效的估计器。
4.2.4 RG-RBM模型
在Mehta和Schwab【2014】的论文中,重整化的概念被用于解释深度学习模型的性能。重整化是一种用于研究物理系统的技术,当无法获取其微观成分的详细信息时,提供了对系统行为的粗略理解跨越不同的长度尺度。
作者提出深度神经网络(DNN)可以看作是迭代的粗粒化方案,类似于重整化群(RG)理论。在这种背景下,神经网络的每一层新高层次都从输入数据中学习越来越抽象和高级的特征。他们认为,深度学习中提取相关特征的过程本质上与统计物理学中的粗粒化过程相同,因为DNN有效地模拟了这一过程。
该论文强调了RG和受限玻尔兹曼机(RBM)之间的密切联系,并提出了物理概念框架与神经网络可能的整合。这种RG与RBM之间的映射提供了统计物理学与深度学习之间关系的洞察。
总体而言,Mehta和Schwab的工作展示了如何应用重整化来理解深度学习模型的性能。它强调了深度学习中的特征提取与统计物理学中的粗粒化过程之间的相似性。RG与RBM之间的映射为物理概念和神经网络的结合提供了潜在的解释。
4.3 耗散结构神经网络
自组织理论认为,当一个开放系统远离平衡态达到非线性区域时,一旦系统的某个参数达到一定阈值,系统就会通过波动发生突变,从无序转变为有序,并产生化学振荡等自组织现象。它由耗散结构(从无序到有序)、协同(系统各元素的协同作用)和突变理论(阈值突变)组成。
自组织特征映射(SOM)【Kohonen 1989, 1990】由Kohonen教授提出,当神经网络接受外部输入时,SOM将分为不同的区域,每个区域对输入模式有不同的
响应特性。它通过自动发现样本中的内在规律和本质属性,自组织和自适应地改变网络参数和结构。自组织(竞争性)神经网络是一种模拟上述生物神经系统功能的人工神经网络。即在学习算法上,它模拟了兴奋、协调和抑制、生物神经元之间的竞争等信息处理的动态原理,指导网络的学习和工作。由于SOM是一种可以可视化高维数据并能有效压缩信息传输的工具,Kohonen等人【1996】总结了一些SOM的工程应用。
耗散结构是在系统远离热力学平衡状态时,在某些外部条件下,由于系统内部的非线性相互作用,通过突变形成了一种新的有序结构,这是非平衡统计物理学分支中的一个重要新方面。2017年,Amemiya等人发现并概述了糖酵解振荡在细胞节律和癌细胞中的作用【Amemiya et al., 2017】。同年,Kondepudi等人讨论了耗散结构在理解生物体中的相关性,并提出了一种电压驱动系统【Kondepudi et al., 2017】,该系统可以表现出类似于我们在生物体中看到的行为。同年,Burdoni和De Wit讨论了反应和扩散之间的相互作用如何在不同反应物接触时产生局部的时空模式【Budroni and De Wit, 2017】。
4.4 随机表面神经网络
在人工智能领域,早期的研究受到凸面优化的理论保证的强烈影响,在凸面优化中,每个局部极小值也是全局极小值【Boyd et al., 2004】。然而,在处理非凸面时,高误差局部极小值的存在可能会影响梯度下降的动态,并影响优化算法的整体性能。
高维空间中光滑随机高斯表面的统计物理学已经被广泛研究,产生了各种表面模型,将空间信息与概率分布连接起来【Bray and Dean, 2007; Fyodorov and Williams, 2007】。这些模型为理解非凸面的行为和特性提供了见解,揭示了高维优化问题所面临的挑战。
在2014年,Dauphin等人研究了神经网络误差表面模型与统计物理学之间的联系,即球形自旋玻璃能量函数与神经网络误差表面模型之间的联系【Choromanska et al., 2015】。
2014年,Pascanu在Dauphin等人【2014】的工作中提出了鞍点无关牛顿算法(SFN),针对高维非凸优化问题中存在大量鞍点而非局部极值的问题。它可以迅速摆脱梯度下降减缓的鞍点。此外,Kawaguchi【2016】将随机表面引入更深层的网络中。
通过研究随机表面的统计物理学,研究人员更好地理解了非凸优化中遇到的复杂景观。这些知识对改进优化算法和增强在高维空间中操作的人工智能系统的性能具有重要意义。
总之,统计物理学研究了不同的表面模型,以分析非凸优化景观的行为。理解这些表面的特性不仅对解决高维优化问题的挑战至关重要,而且对改进人工智能算法的性能也具有重要意义。
4.5 自由能表面(FES)神经网络
自由能是指在特定热力学过程中,系统的减少的内能中能够转化为外界功的一部分。它衡量了系统在特定热力学过程中可以向外输出的“有用能量”。自由能可以分为亥姆霍兹自由能和吉布斯自由能。配分函数等同于自由能。
在基于能量的模型中,研究人员提出了许多方法来克服计算自由能的困难。这些方法包括穷尽蒙特卡洛法、对比散度启发式【Hinton, 2002】及其变体【Tieleman and Hinton, 2009】、分数匹配【Hyvärinen and Dayan, 2005】、伪似然【Besag, 1975】以及最小概率流学习(MPF)【Battaglino, 2014; Sohl-Dickstein et al., 2011】(其中MPF本身基于非平衡统计力学)。尽管取得了这些进展,在高维数据集上训练具有表现力的基于能量的模型仍然是一个未解决的挑战。
在基于能量的模型中,提出了几种方法来应对计算自由能的挑战。这些方法旨在尽管估计自由能存在计算困难,仍然有效地训练模型。一些值得注意的方法包括:
穷尽蒙特卡洛法:该方法使用蒙特卡洛技术从模型的分布中进行采样,对于高维数据集来说,这可能是计算量很大的。
对比散度(CD)及其变体:CD是Hinton【2002】提出的用于训练基于能量模型的流行启发式方法。它通过进行几步吉布斯采样来近似模型参数的梯度。CD的变体,例如持久对比散度(PCD)【Tieleman and Hinton, 2009】,旨在通过保持持久链的样本来改进训练过程。
分数匹配:这一方法由Hyvärinen和Dayan【2005】提出,涉及通过匹配模型分布的矩和数据分布的矩来估计模型的参数。
伪似然:由Besag【1975】提出,该方法通过考虑每个变量给定其他变量的条件概率来近似模型的似然。
最小概率流学习(MPF):MPF基于非平衡统计力学,是Battaglino【2014】和Sohl-Dickstein等人【2011】提出的一种训练基于能量模型的技术。它通过流动动力学最小化模型分布和数据分布之间的差异。
机器学习方法将系统的自由能表面作为集体变量的函数进行学习,以优化人工智能算法。通过神经网络的自由能表面表示,可以改进高维空间的采样。例如,Schneider等人提出了一种可学习的自由能表面,用于预测压力下固体氙的NMR自旋自旋耦合模型【Schneider et al., 2017】。在2018年,Sidky等人提出了一个用于自由能表面的小型神经网络,它可以使用动态(实时)自适应采样生成的数据点进行迭代训练【Sidky and Whitmer, 2018】。该模型验证了当生成新数据时,可以获得全配置空间的平滑表示。Wehmeyer和Noé【2018】提出了一种时间滞后自编码器方法,用于在肽折叠的示例中识别缓慢变化的集体变量。2018年,Mardt等人提出了一种基于变分神经网络的方法,用于识别蛋白质折叠模拟期间的重要动态过程,并提供了统一的坐标变换和自由能表面探索的框架【Mardt et al., 2018】,提供了对系统底层动态的见解。2019年,Noé等人提出使用玻尔兹曼生成器采样集体空间的平衡分布,以表示自由能表面上的状态分布【Noé et al., 2019】。
尽管取得了这些进展,在高维数据集上训练具有表现力的基于能量的模型仍然是一个挑战性任务。正在进行的研究旨在开发更高效和更有效的训练方法,以应对该领域的未解决挑战。
4.6 知识蒸馏优化神经网络
对于神经网络:模型越大,层数越深,学习能力越强。为了从大量冗余数据中提取特征,CNN通常需要过多的参数和更大的模型进行训练。然而,模型结构的设计难以设计,因此模型优化成为解决这一问题的重要因素。
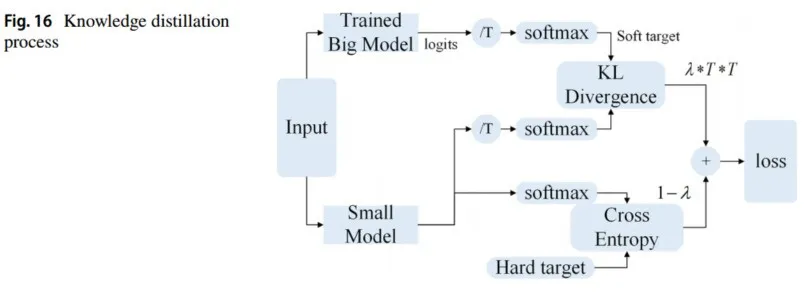
知识蒸馏 在2015年,Hinton的开创性工作“知识蒸馏”(Knowledge Distillation, KD)推动了模型优化的发展【Hinton et al., 2015】。知识蒸馏模拟物理中的加热蒸馏以提取有效物质,并将大模型(教师网络)的知识转移到小模型(学生网络),从而使模型更易于部署。在蒸馏过程中,小模型学习大模型的泛化能力,加快推理速度,并保留接近大模型的性能(图16)。
4.6.1 知识蒸馏神经网络
2017年,TuSimple和Huang等人提出了一种蒸馏算法,利用神经元的知识选择特性来传递新知识(对齐选择风格分布),并命名为神经元选择性转移(Neuron Selectivity Transfer, NST)【Huang and Wang, 2017】。NST模型可以与其他模型结合,学习更好的特征并提高性能。为了使学生网络能够自动从教师网络中学习到良好的损失函数,以保留类别之间的关系并保持多样性,Zheng等人在2018年使用条件对抗网络(Conditional Adversarial Networks, CAN)构建了教师-学生架构【Xu et al., 2017】。深度互学习(Deep Mutual Learning, DML)模型【Zhang et al., 2018】和再生神经网络(Born Again Neural Networks, BAN)模型【Furlanello et al., 2018】于2018年提出,它们应用了知识蒸馏,但并不旨在压缩模型。Huang等人【2024】提出了一种新的知识蒸馏模型,使用扩散模型来显式去噪和匹配特征,从而降低计算成本。Ham等人【2024】提出了一种基于知识蒸馏对抗训练策略的新型网络,命名为NEO-KD,能够提高对抗攻击的鲁棒性。
4.6.2 网络架构搜索(NAS)和知识蒸馏(KD)
知识蒸馏将教师网络中的知识转移到学生网络中,而NAS中存在大量的网络,使用知识蒸馏有助于提高超级网络的整体性能。2020年,Peng等人提出了一种基于优先路径的网络蒸馏算法,以解决模型之间权重共享的固有缺陷,即HyperNetworks中子网训练不足的问题【Peng et al., 2020】,从而改善了各个模型的收敛性。同年,Li等人使用Distill the Neural Architecture(DNA)算法【Li et al., 2020】,通过知识蒸馏来监督网络内部结构的搜索,这显著提高了NAS的有效性。Wang等人【2021】通过自适应选择alpha散度改进了KL散度,有效防止了教师模型中的过度估计或不确定性估计。Gu和Tresp【2020】结合了网络剪枝和蒸馏学习,以搜索最适合的学生网络。Kang等人在【2020】中提出了Oracle Knowledge Distillation(OKD)方法,从综合教师网络中进行蒸馏,并使用NAS调整学生网络模型的容量,从而提高了学生网络的学习能力和学习效率。受到BAN的启发,Macko等人【2019】提出了自适应知识蒸馏(Adaptive Knowledge Distillation, AKD)方法,以辅助子网络的训练。为了提高知识蒸馏的效率和有效性,Guan等人【2020】使用可微分特征聚合(Differentiable Feature Aggregation, DFA)来指导教师网络和学生网络的学习(网络架构搜索),并采用类似于可微分架构搜索(Differentiable Architecture Search, DARTS)的方法【Liu et al., 2018】自适应地调整缩放因子。
4.7 深度神经网络解决经典统计物理问题
4.7.1 魔方问题
魔方由Rubik教授于1974年发明,最初称为“魔术方块”。后来,这款玩具由Ideal Toy Co发行,并被命名为“Rubik's Cube”(Rubik魔方)【European, Plastics, News, group (2015)】。2018年,一个名为DeepCube的新算法无需人工协助,通过自学推理解决了魔方问题【McAleer et al., 2018】。这是在尽量减少帮助的情况下解决复杂问题的里程碑。2019年,Agostinelli等人在《Nature Machine Intelligence》上提出使用DL方法DeepCubeA和搜索算法解决魔方问题【Agostinelli et al., 2019】。DeepCubeA可以在没有任何特定领域知识的情况下学会如何解决魔方问题,并能够从目标状态反向解决越来越困难的魔方问题。2021年,Corli等人引入了一种基于哈密顿奖励的深度强化学习算法,并引入了量子力学来解决魔方组合问题【Corli et al., 2021】。诺丁汉大学的副教授Colin的团队在《Expert Systems》上发表了一篇论文,使用逐步深度学习方法学习“适应度函数”来解决魔方问题,并强调了逐步处理的优势【Johnson (2021)】。
4.7.2 神经网络检测相变
由于深度神经网络(DNN)的每一个新的高层都能从数据中学习到越来越抽象的高级特征,而前几层则可以学习更精细的尺度以表示输入数据,研究人员引入了重整化理论并从微观规则中提取宏观规则。2017年,Bradde和Bialek讨论了重整化群和主成分分析之间的类比【Bradde and Bialek (2017)】。2018年,Li和Wang等人使用神经网络学习了一种新的重整化方案【Koch-Janusz and Ringel (2018); Kamath et al. (2018)】。
相变是物质不同相之间的边界,通常由序参量来表征。然而,神经网络展示了能够学习适当的序参量并在不需要先验物理知识的情况下检测相变的能力。2018年,Morningstar和Melko使用无监督生成图理解二维伊辛系统的概率分布,这项工作展示了神经网络可以捕捉伊辛模型中相变的基本特征【Morningstar and Melko (2017)】。
文献中还提供了神经网络能够区分伊辛模型中相变的正面证据。Carrasquilla和Melko【2017】,以及Wang【2016】利用主成分分析在无需先验系统物理特性的情况下检测相变。Tanaka和Tomiya【2017】提出了一种通过热图估计特定相边界值的方法,进一步展示了在不需要先验物理系统知识的情况下发现相变现象的可能性。
对于这些主题的深入理解,感兴趣的读者可以参考Kashiwa等人的论文【2019】和Arai等人的论文【2018】。总的来说,这些研究强调了神经网络即使在没有明确物理知识的情况下,也有可能识别和表征相变现象,开辟了研究复杂系统和发现涌现现象的新途径。
4.7.3 蛋白质序列预测与结构建模
蛋白质序列预测和结构建模在“AI + 大健康”领域,如精准医学和药物研发中,具有重要意义。2003年,Bakk和Høye通过引入简化的一维蛋白质类比(即使用一维伊辛模型)研究了蛋白质折叠问题【Bakk and Høye (2003)】。最近,Cocco等人【2018】使用随机受限玻尔兹曼机(RBM)模型对蛋白质家族的序列信息进行了建模【Tubiana et al., 2019】。RBM学习过程的分析研究极具挑战性,通常使用基于吉布斯采样的对比散度算法【Hinton (2002)】。
Wang等人【2018】利用卷积神经网络结合极限学习机(ELM)分类器预测RNA-蛋白质相互作用。2019年,Brian Kuhlman等人回顾了用于蛋白质序列预测和三维结构建模问题的深度学习方法【Kuhlman and Bradley (2019)】。在《Nature Communications》中,Ju等人引入了一种新的神经网络架构CopulaNet,该架构可以从目标蛋白质的多序列比对中提取特征并推断残基共进化,克服了传统统计方法中的“信息丢失”缺陷【Ju et al., 2021】。
4.7.4 有序玻璃状结构设计
Mehta在【Bukov et al., 2018】中的实验提供了这一方向的一些初步思路,突出了强化学习在量子物理学之外的平衡量应用中的潜在用途。2019年,Greitemann和Liu等人引入并研究了一种基于核学习的方法【Greitemann et al., 2019; Liu et al., 2019】,用于学习受挫磁性材料中的相位,具有更容易解释和识别复杂序参量的能力。
2016年,Nussinov等人也研究了有序玻璃状固体,使用多尺度网络聚类方法来识别玻璃的空间和时空结构【Cubuk et al., 2015】,学习识别结构流动缺陷。还可以辨别出广泛无序材料中观察到的异质动态所负责的微妙结构特征。2017年,Wetzel等人将无监督学习应用于伊辛模型和XY模型【Wetzel (2017)】,2018年,Wang和Zhai等人在受挫自旋系统中引入了无监督学习【Wang and Zhai (2017); Wang and Zhai (2018)】,超越了监督学习的局限性,能够更好地进行分类。
4.7.5 非线性动力系统的预测
人工智能还提供了稳健的系统来研究、预测和控制非线性动力系统。2016年,Reddy等人使用强化学习教会自主滑翔机利用大气中的热能像鸟一样飞行【Reddy et al., 2016; Reddy et al., 2018】。2017年,Pathak等人使用一种称为回声状态网络的递归神经网络或库(Jaeger和Haas,2004)来预测混沌动力系统的轨迹,并建立了用于天气预报的模型【Pathak et al., 2018】。Graafland等人【2020】使用BNS建立数据驱动的复杂网络来解决气候问题。相关网络(CNS)的网络拓扑结构包含冗余信息。另一方面,贝叶斯网络(BNS)只包含(从概率的角度看)非冗余信息,因此可以利用稀疏拓扑结构从中提取出有信息的物理特征。Boers等人【2014】使用极端事件同步方法研究了极端降水的全球模式,并尝试预测南美洲的降水。Ying等人【2021】使用相同的方法研究了碳循环和碳排放,制定了碳排放和碳减排的策略和对策。Chen等人【2021】将本征微态方法应用于不同结构上臭氧的分布和演变。Zhang等人【2021】通过考虑地震的长期记忆模型,改变了传统的ETAS地震预测模型。海洋混合参数的不确定性是海洋和气候建模中偏差的主要来源,缺乏过程理解的传统物理驱动参数化方法在热带表现不佳。Zhu等人【2022】探索了利用深度学习方法和长期湍流测量的海洋垂直混合过程参数化的数据驱动方法,在有限观测数据下展示了良好的性能、良好的物理约束泛化能力,并改善了气候模拟中的物理信息。
5 受量子力学启发的深度神经网络范式
量子算法是一类在量子计算模型上运行的算法。通过借鉴量子力学的基本特性,如量子叠加或量子纠缠,量子算法在计算复杂性上相比传统算法具有显著的减少,甚至可以达到指数级的降低。早在1992年,David Deutsch和Richard Jozsa提出了第一个量子算法,即Deutsch-Jozsa算法【Deutsch and Jozsa (1992)】。该算法仅需要一次测量就可以确定Deutsch-Jozsa问题中未知函数所属的类别。虽然这个算法缺乏实际应用,但它引发了一系列后续的传统量子算法。1994年,Peter W. Shor提出了著名的量子大数质因数分解算法,称为Shor算法【Shor (1994)】。传统分解算法的计算复杂性随着问题规模呈指数级增长,而Shor算法可以在多项式时间内解决质因数分解问题。1996年,Lov K. Grover提出了经典的量子搜索算法,也称为Grover算法,其复杂度为O(√N),相比传统搜索算法提高了二次效率【Grover (1996)】。受自然启发的随机优化算法一直是研究的热点话题。近期的工作【Sood (2024)】对量子启发的元启发式算法进行了全面概述,而【Kou et al. (2024)】的工作总结了量子动态优化算法。表4中概述了这些代表性方法。
5.1 量子机器学习
量子机器学习(Quantum Machine Learning,QML)结合了量子计算的速度和机器学习提供的学习和适应能力。通过模拟微观粒子所具有的叠加、纠缠、一致性和平行性特性,将传统的机器学习算法量子化,以增强其表示、推理、学习和数据关联的能力。
通常,量子机器学习算法有以下三个步骤:(1) 量子态准备。利用量子计算的高度并行性,原始数据必须转换为量子比特的形式,使数据具有量子特性;(2) 量子算法处理。量子计算机不再属于冯·诺依曼架构,其操作单元与传统计算机完全不同,因此需要将传统算法量子化并移植到量子计算机上。算法的移植应结合传统算法的数据结构和量子理论的特性,以有效加速传统算法,使量子算法的使用具有意义;(3) 量子测量操作。结果以量子态的形式输出,它本身以概率形式存在。通过量子测量,量子叠加波包坍缩为经典态,从而提取量子态中包含的信息以供后续信息处理。
量子机器学习的历史可以追溯到1995年,当时Subhash C. Kak首次引入了“量子神经计算”的概念【Kak (1995)】。Kak认为量子计算机是一个可以响应刺激并重新组织自身以执行高效计算的常规计算机集合。与传统机器学习算法一样,量子机器学习算法可以根据数据格式进行分类:量子无监督学习和量子监督学习。
5.1.1 量子无监督学习算法
量子K均值算法 聚类算法是无监督学习算法中最重要的一类之一。聚类是指根据某些特定标准(例如距离标准)将一些样本在没有标签的情况下划分为不同的类或簇,使得同一簇中样本之间的差异尽可能小,而不同簇中样本之间的差异尽可能大。
对于无监督聚类算法,K均值算法是最常见的一种。其核心思想是,对于一个由
个无标签样本组成的数据集和
个聚类(
),根据样本与簇中心之间的距离,每个样本被分配到最近的簇中:

其中,
表示待聚类的样本,
表示类别
中第
个样本。然后所有簇的中心点会迭代更新,直到中心位置收敛。由于在执行K均值算法时,必须测量每个样本与每个簇中心之间的距离并更新所有簇的中心,因此当样本数量和簇数量较大时,K均值算法的时间成本会非常高。
2013年,Lloyd等人(2013)提出了量子版的Lloyd算法,用于执行K-Means算法。该算法的主要思想与传统的K-Means算法相同,即比较量子态之间的距离,但Hilbert空间中的量子态既具有纠缠性又具有叠加性,并且可以在并行处理中同时处理多个样本,以获得样本所属的聚类。
首先,算法需要将样本转换为量子态
。纠缠态
和
定义如下:
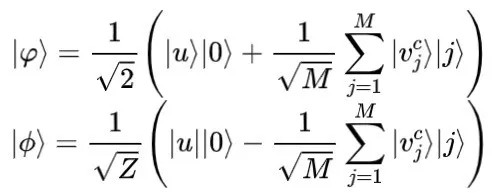
其中
为归一化因子。可以证明,待测样本和聚类中心之间的期望距离
等于
乘以成功测量概率:
可以被认为是
在
方向上的投影模平方,可以通过成功执行Swap量子操作的概率来获得。该算法的步骤对于样本空间中的每个样本只执行一次,以找到离样本最近的聚类并将样本分配到该聚类。
5.1.1 量子无监督学习算法
量子k-means算法
聚类算法是无监督学习算法中最重要的类别之一。聚类是指根据一些特定的标准(例如距离标准)将一些样本划分为不同的类或簇,使得同一簇内样本之间的差异尽可能小,而不同簇间样本之间的差异尽可能大。
对于无监督聚类算法,K-means算法是最常见的一种。其核心思想是,对于一个由
个无标签样本组成的数据集,假设有
个聚类(
),根据样本与各个聚类中心之间的距离,每个样本被分配到最近的聚类:
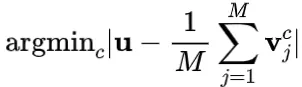
其中
表示待聚类的样本,
表示类
中第
个样本。然后所有聚类的中心会反复更新,直到中心的位置收敛。由于在执行K-means算法时需要测量每个样本与每个聚类中心的距离并更新所有聚类的中心,当样本数量和聚类数量很大时,K-means算法的时间成本将非常高。
2013年,Lloyd等人提出了Lloyd算法的量子版本来执行K-means算法。该算法的主要思想与传统的K-means算法相同,都是比较量子态之间的距离,但是Hilbert空间中的量子态同时具有纠缠和叠加性质,并且可以并行处理,以获得聚类样本的归属。首先,算法需要将样本转换为量子态
。纠缠态
和
定义为:
其中
是归一化因子。可以证明,样本与聚类中心之间的期望距离
等于
乘以测量成功的概率:
可以看作是
在
方向上的投影模的平方,这可以通过成功执行交换量子操作的概率获得。这种算法的步骤只对样本空间中的每个样本执行一次,以找到与样本距离最近的聚类,并将样本分配到最近的聚类中。
量子主成分分析
降维算法是最重要的无监督学习算法之一。这些算法将高维空间中样本的特征映射到低维空间。样本的高维表示包含噪声信息,这会导致误差和精度的下降。通过降维算法,可以减少噪声信息,这有助于获取样本的基本特征。
在降维算法中,主成分分析(PCA)是最常见的算法之一。PCA的思想是通过线性投影
将样本矩阵
的高维特征映射到低维表示
,以便投影空间中特征的方差最大化,并且每个维度之间的协方差最小化,即
的协方差矩阵
对角化。可以证明,矩阵
是样本矩阵
的协方差矩阵
的特征矩阵。通过这种方式,使用更少的维度保留原始样本的更多属性,但是当面对大量高维向量时,PCA的计算成本非常高。
2014年,Lloyd等人提出了量子主成分分析(QPCA)算法。QPCA可以用于量子态的判别和分配。假设存在两个集合,由
个状态组成,并从中采样,密度矩阵
从第一个集合
中获得,密度矩阵
从第二个集合
中获得。假设需要分配的量子态为
,可以通过密度矩阵连接以及量子相位估计来获得
的特征向量和特征值:
其中
和
分别是
的特征值和特征向量。通过测量特征值
,如果特征值为正,则
属于第一类
,如果特征值为负,则属于第二类
。以上过程是最小错误态判别,并且具有指数级的加速效果。QPCA假设通过QRAM来准备量子态,但QRAM目前仅是一个理论模型,还没有实际的物理实现。
5.1.2 量子监督学习算法
量子线性判别分析 类似于PCA,线性判别分析(LDA)也是一种降维算法。但与PCA算法不同,PCA算法减少未标记样本数据的维度,而LDA则减少标记样本数据的维度。LDA算法的思想是将数据投影到低维空间,并使同一类的投影数据尽可能接近,即最小化类内散度:
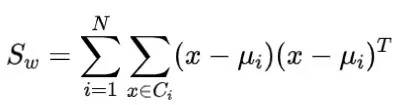
并使得类间中心的距离尽可能大,即最大化类间散度:
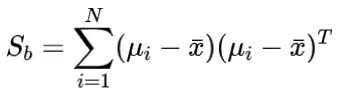
为了同时满足这两个条件,有必要最大化广义Rayleigh商:
其中,
是投影超平面的法向量。这个优化问题可以通过拉格朗日乘子法解决。
在2016年,Cong和Duan(2016)提出了量子线性判别分析(QLDA)算法。与经典的LDA算法相比,QLDA实现了指数级的加速,这极大地减少了计算难度和空间利用。首先,QPCA使用Oracles算子来获取密度矩阵:
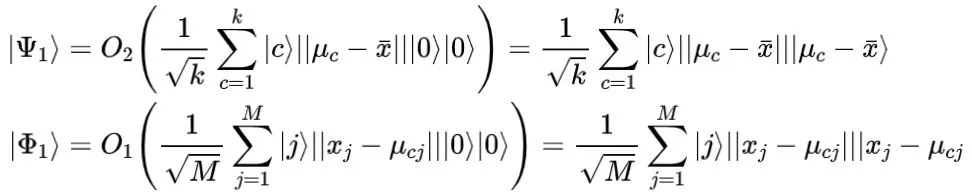
如果向量的范数形成有效的生产分布,则可以获得状态:
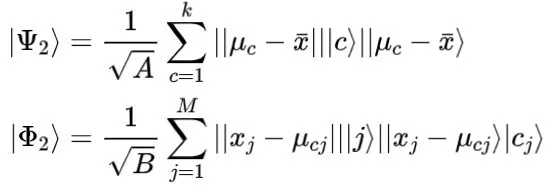
其中
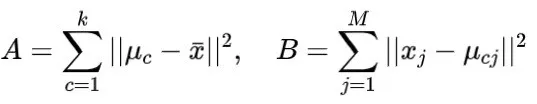
在对由两个状态
,
组成的密度矩阵执行偏置迹操作后,可以得到公式 (26):
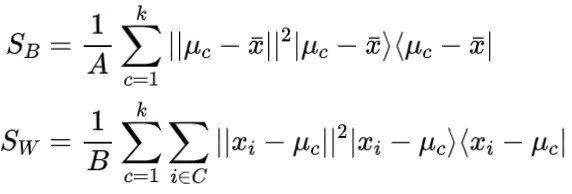
可以通过拉格朗日乘数法求解公式 (26),并得到解。可以通过量子相位估计法获得
的特征值和特征向量。最终,最佳投影方向
通过 Ermey 矩阵连接解得出。
该算法与QPCA算法类似。它们都将原问题中样本的协方差矩阵与量子系统的密度矩阵相关联,并研究密度矩阵的特征值和特征向量,以获得最佳投影方向或主特征向量。
量子k近邻(Quantum k-nearest neighbors,QKNN)算法是一个非常经典的分类算法。该算法为待分类样本
寻找距离最近的
个已标记样本,然后根据这
个样本的标签,使用分类决策规则(例如多数投票)来决定
属于哪个类别。KNN算法的优点在于,当数据集足够大时,算法的准确性将非常高,但当数据库规模较大或样本的维度较高时,计算成本将会非常高。
2014年,Wiebe等人提出了量子k近邻算法(Quantum K-Nearest Neighbor algorithm,QKNN)。该算法可以通过内积获得欧几里得距离,与蒙特卡罗算法相比,该方法在查询复杂度上有多项式级别的减少。QKNN算法首先将向量
、
的非零数据编码为量子态
、
的概率幅值:
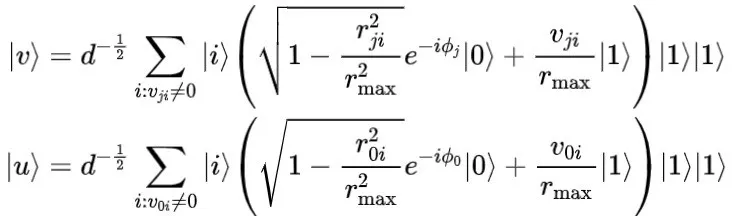
其中,
,
,
是特征值的上界,内积可以通过对
、
进行SWAP操作得到:
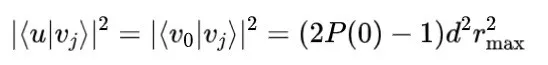
其中,
表示测量结果为零时的概率。Wiebe等人还尝试使用两个量子态的欧几里得距离来确定它们的分类规则,但实验结果表明,这种方法比内积方法迭代次数更多,且精度更低。因此,量子欧几里得距离分类算法并未得到推广。
量子决策树分类器 决策树(Decision Tree, DT)算法是一种经典的监督学习模型。DT算法表示对象属性与类别之间的映射关系。树中的节点表示属性值,决定分类的方向。从根节点到叶节点的每一条路径代表属性值要求,依据这些要求可以将对象识别为某一类别。该算法利用样本学习决策树的结构和判别规则,用于样本分类。为了提高DT的学习效率,通常使用信息增益来选择关键特征(如表5所示)。
在2014年,Lu和Braunstein提出了一种量子决策树(QDT)分类器,该分类器通过量子态之间的保真度度量将样本聚类为子类,从而使QDT可以控制量子态。此外,他们提出了一个量子熵杂质准则来修剪决策树。QDT分类器首先将样本特征
转换为量子态
,其中
表示对应于第
个样本的
量子态,
表示对应于样本
的已知类别的量子态。量子熵杂质准则定义为:
其中是对应于节点
的量子态密度矩阵。
表示矩阵的迹数(或迹值),即主对角线上元素的和。准则的期望值计算为:

最后,使用Grover算法来求解方程(31)中的期望值最小值,期望值对应的类别即为样本所属的类别。在该算法中,经典信息论中的Shannon熵被量子熵杂质准则所替代,通过计算准则的期望值可以获得特征值,这就是该算法与传统决策树算法的区别。
5.1.3 量子支持向量机(Quantum Support Vector Machine)
支持向量机(Support Vector Machine, SVM)是一个重要的监督线性分类算法。SVM的思想是通过找到最大间隔的分类超平面进行分类:
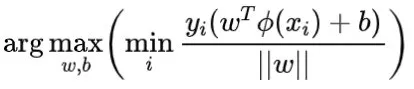
其中
是超平面的法向量,
是偏差,
是样本
的标签。
对应的解称为支持向量,它是最接近分类超平面的样本,并且 是从样本到超平面的最大间隔。通过尺度变换可以得到以下方程:
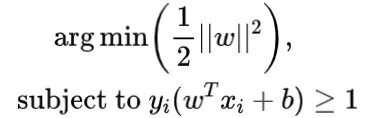
该方程是一个条件约束问题,可以通过拉格朗日乘子法求解。
2014年,Rebentrost等人(2014年)提出了量子支持向量机 (QSVM)。QSVM 使用非稀疏矩阵指数化技术来有效地执行矩阵求逆,并获得指数加速。QSVM 首先使用 Oracles 运算符将特征向量编码为量子态概率幅值:
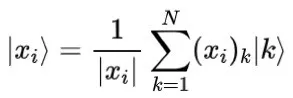
为了获得归一化的核矩阵,需要得到量子态:
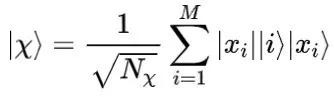
其中
。归一化的核矩阵可以通过密度矩阵
的偏差迹求解:
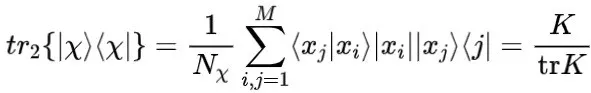
通过这种方法,量子系统与传统机器学习中的核矩阵相关联。由于量子态之间进化运算的高度并行性,传统机器学习中的核矩阵的计算可以得到加速。
5.2 量子深度学习
与量子机器学习类似,量子深度学习(QDL)使得深度学习算法能够利用量子力学的基本性质。QDL使用量子计算代替传统的冯·诺依曼计算,从而使深度学习算法量子化,显著提高算法的并行性,减少计算复杂性。
神经元的基本原理是通过权重参数模拟兴奋或抑制的信号,并通过连接权重模拟信息处理,以获得输出。因此,可以将神经元建模为:
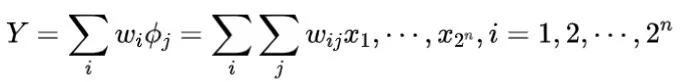
其中
表示输入节点的数量。
如果量子态
是正交的,则可以通过量子幺正变换表示神经元的输出:
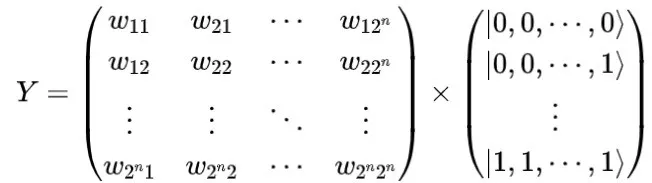
一般来说,训练量子神经元模型的过程涉及五个步骤:首先,初始化权重矩阵
;第二,根据问题构造训练集
;第三,计算神经元输出
,其中
是迭代次数;第四更新权重参数。最后,重复第三和第四步,直到网络收敛。
量子神经计算的概念是由Kak在1995年提出的,但量子深度学习的概念最早是在2014年由Wiebe等人提出的。Schuld等人在2014年提出了满足量子神经网络的三个要求:第一,量子系统的输入和输出被编码为量子态;第二,量子神经网络反映了一个或多个基本神经计算机制;第三,基于量子效应的演化必须完全兼容量子理论。
5.2.1 量子多层感知器
在1995年,Mennee和Narayanan提出了量子启发神经网络(QUINN)。传统神经网络训练神经网络以找到使网络能够为每个模式获得正确结果的参数。受量子叠加性启发,QUINNs训练多个同构神经网络,这些网络仅为每个模式处理一个单一模式,并且与不同模式对应的同构网络以量子方式叠加以生成QUINNs。QUINNs的权重向量被称为量子启发波函数(QUIWF),在测量时会发生坍缩并生成分类结果。
在1996年,Behrman等人提出了量子点神经网络(QDNN)。QDNN模拟一个与时间变化场耦合到衬底晶格的量子点分子,并使用时间维度的离散节点作为隐藏层神经元。研究表明,QDNN可以在相空间的某些区域执行任何所需的经典逻辑门。
在1996年,Tóth等人提出了量子细胞神经网络(QCN)。QCN使用细胞形成相互作用的量子点,这些量子点通过库仑力在细胞之间通信,每个细胞编码一个连续的自由度,其状态方程可以用时间依赖的薛定谔方程来描述细胞网络。
在2000年,Matsui等人提出了一种基于量子电路的量子神经网络。网络的基本单元是由1比特旋转门和2比特控制非门组成的量子逻辑门,这些逻辑门可以实现所有基本的逻辑操作。它通过旋转门的控制和神经元内的计算来控制神经元之间的连接。由于神经元的构造依赖于量子逻辑门,当网络结构复杂时,逻辑门的数量将以指数级增加。
在2005年,Kouda等人构建了一个带有量子逻辑门的量子比特神经网络,并提出了量子感知器的结构。接受来自其他
个神经元输入的神经元状态
表示为:
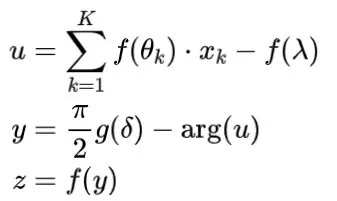
其中,量子态
,
表示激活函数,
表示
的相位角。
在2006年,Zhou等人提出了量子感知器网络(QPN)。通过实验模拟,包含仅一个神经元的量子感知器仍然可以实现不同类别的操作,而这种操作是传统的仅包含一个神经元的感知器无法实现的。QPN的结构如下:
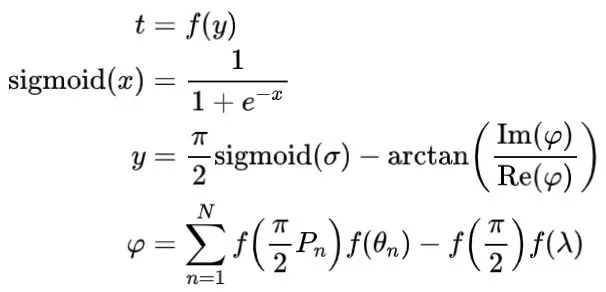
其中,
和
分别是加权参数和相位参数,
是相位控制因子,
是输入数据。
在2014年,Schuld等人提出了一种基于量子行走的量子神经网络。该网络利用量子行走的位置来表示二进制神经元的发射模式(休息和激活状态),这些状态编码为一组二进制字符串。为了模拟神经网络的耗散动力学,网络执行量子行走,以去相干的方式实现对非完全初始化模式的记忆检索。
5.2.2 量子循环神经网络
2014年,Wiebe等人首次提出了“量子深度学习”的概念。他们认为,量子算法可以有效解决一些传统计算机无法解决的问题。量子算法为深度学习提供了一个更高效和全面的框架。此外,他们还提出了一种量子玻尔兹曼机的优化算法,减少了玻尔兹曼机的训练时间,并显著改善了目标函数的表现。
玻尔兹曼机(BM)是一种无向的循环神经网络。从物理的角度来看,BM是基于热平衡的伊辛模型建模的,并使用吉布斯分布来建模每个隐藏节点的概率。他们提出了两种量子方法来解决BM的优化问题:通过量子采样进行梯度估计(GEQS)和通过量子幅度估计进行梯度估计(GEQAE)。GEQS算法使用平均场理论来近似每个配置的非均匀先验分布,并从平均场状态中提取吉布斯态,从而在两种状态足够接近时准确地准备吉布斯分布。与GEQS算法不同,GEQAE使用Oracle算子对训练数据进行量子化,其思想是在量子中使用幅度估计对样本进行编码,大大降低了梯度估计的计算复杂度。
2020年,Bausch提出了量子循环神经网络(QRNN),主要由一种新型的量子神经元构成。该神经元的非线性激活函数通过量子比特基向量旋转时产生的振幅变化所引起的余弦函数的非线性来实现。这些神经元组合形成一个结构化的QRNN单元,通过迭代得到类似于传统循环神经网络(RNN)的循环模型。
2020年,Chen等人提出了量子长短期记忆网络(QLSTM)。QLSTM利用具有可调参数的变分量子电路(VQC)来替代传统神经网络中的LSTM单元。VQC具有特征提取和数据压缩的能力,由数据编码层、变分层和量子测量层组成。通过数值模拟可以证明,QLSTM的学习速度更快,收敛更稳健,并且不像传统LSTM那样出现典型的损失函数尖峰。
2021年,Ceschini等人提出了一种在量子框架中实现LSTM单元的方法。该方法使用量子电路来复制单元的内部结构以进行推理。在此方法中,提出了一种编码方法来量子化LSTM单元的算子,如量子加法、量子乘法和量子激活函数。最后,通过在IBM Quantum Experience™平台和经典设备上的数值模拟验证了该量子架构。
5.2.3 量子卷积网络
2019年,Cong等人首次提出了量子卷积神经网络(QCNN)。QCNN是一个变分量子电路模型,其输入是一个未知的量子态。卷积层由参数化的双量子比特门构成,以平移不变的方式应用单个准局部酉算子。池化操作通过根据部分量子比特的测量结果对附近量子比特应用酉旋转来实现。卷积和池化层依次执行,直到系统规模足够小,以获得量子比特作为输出。与传统卷积神经网络类似,QCNN的卷积和池化层中的超参数是固定的,而QCNN的卷积和池化层中的参数是可学习的。
2020年,Iordanis Kerenidis等人提出了模块化量子卷积神经网络算法,该算法通过简单的量子电路实现所有模块。该网络能够实现任意层数以及任意数量和大小的卷积核。在前向传播过程中,QCNN相较于传统的CNN具有指数级的加速效果。
2021年,Liu等人提出了混合量子-经典卷积神经网络(QCCNN)。QCCNN利用交错的1量子比特层和2量子比特层来形成量子卷积层。1量子比特层由包含可调参数的Ry门组成。2量子比特层由最近邻对的量子比特上的CNOT门组成。QCCNN通过量子卷积层将输入转换为可分离的量子特征,利用池化层来降低数据的维度,最后测量量子特征以获得输出标量。
5.3 量子进化算法
进化算法是一种基于达尔文自然选择理论和孟德尔遗传变异理论构建的随机搜索算法,模拟生物进化中的繁殖、突变、竞争和选择过程。量子进化算法使用量子比特来编码个体,并通过旋转门和非门来更新个体,使得个体能够同时包含多个状态的信息,从而获得更丰富的种群,大大提高了算法的并行性和收敛速度。
在量子进化算法中,每个个体都用量子比特进行编码。编码后,个体的每个基因都包含了处于叠加态的全部信息:
其中,
和
表示满足
的量子态的概率幅度,因此用量子比特编码的个体可以表示为:
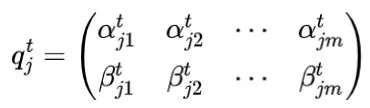
其中,
表示第
次迭代后种群中的第
个个体,
表示个体中的基因数量。用量子比特编码的个体可以同时表达多个量子态的叠加,使得个体更加多样化。随着算法的收敛,
和
也将收敛到0或1,使得编码的个体最终收敛为单一状态。
通常,量子进化算法有以下步骤:首先,初始化种群以确保
;其次,生成随机数
,并将
与量子态
的概率幅度进行比较,量子态的测量值为1当且仅当
,否则该值取0。这样,每个个体在种群中被测量一次以获得一组种群解;第三,评估每个状态的适应度;第四,将当前种群的最佳状态与记录的历史最佳状态进行比较,然后记录最佳状态和适应度;第五,利用量子旋转门和量子非门(NOT)按照某种策略更新种群;最后,循环上述步骤,直到收敛条件达到。
最早的量子进化算法由Narayanan和Moore(1996)提出。1996年,他们首次将量子理论与遗传算法相结合,提出了量子遗传算法,开创了量子进化计算的领域。量子进化算法由Han等人提出。基于并行量子启发式遗传算法(PGQA)的基础上,Han等人(2001年)提出了量子进化算法,并在2002年将量子遗传算法扩展到量子进化算法(QEA)。
5.3.1 量子编码算法
2008年,Li 和 Li 提出了基于 Bloch 球坐标编码的量子进化算法。在该算法中,个体使用量子比特的 Bloch 坐标进行编码,通过量子旋转门进行更新,并通过量子非门(NOT)进行变异。与简单遗传算法(SGA)相比,该算法具有更高的有效性和可行性。同年,Cruz 等人提出了一种基于实数编码的量子进化算法。该算法使用搜索空间中的一个区间来表示量子个体中的基因,并通过脉宽值和种群中量子个体的总数计算脉冲高度,从而确保用于生成经典个体的概率密度函数的总面积等于1。与类似算法相比,该算法可以以较少的计算量获得更好的解,极大地减少了收敛时间。2009年,Zhao 等人提出了一种实数编码混沌量子启发式遗传算法(RCQGA)。RCQGA 将个体映射到解空间中的量子比特,并应用交叉和变异操作来搜索实际个体。表示网络权重的个体被编码为可调矢量,这些矢量可以通过 RCQGA 获得。与类似算法相比,该算法在搜索模糊神经网络的最佳权重时收敛速度更快。2016年,Joshi 等人提出了一种自适应量子进化算法(ARQEA),该算法使用实数进行编码。该算法利用受旋转门启发的无参数量子交叉操作符生成新的种群,并通过量子相位旋转门放大振幅以搜索所需的元素。该算法可以避免进化参数的调整。
5.3.2 量子进化算子
2002年,Li 和 Zhuang 提出了一种基于量子概率表示的遗传算法(GAQPR),其中设计了新颖的交叉算子和变异算子。交叉算子通过交换当前进化目标和更新个体,使个体包含最佳进化信息,而变异算子通过随机选择每个个体的一个量子比特来交换概率幅度。GAQPR 算法对多峰优化问题更为有效,这通过两个典型的函数优化问题得到了证明。2004年,Yang 等人提出了一种基于量子个体的新型离散粒子群优化算法。该算法将每个粒子定义为一个量子比特,并使用随机观测代替 Sigmoid 函数逐步逼近最优结果。该算法在仿真实验和 CDMA 应用中也证明了其有效性。2015年,Jin 和 Jin 提出了一种用于视觉特征选择(VFS)的改进量子粒子群算法(IQPSO)。该算法基于解的反转操作获取反向解,并通过计算所有解和反向解的适应度函数,选择个体最优解和全局最优解。2019年,Rehman 等人提出了一种改进的量子粒子群算法。该方法通过随机选择最佳粒子参与当前搜索域来改变平均最佳位置,然后添加增强因子以提高全局搜索能力,从而找到全局最优解。
5.3.3 量子免疫算子
2008年,Li 等人提出了一种量子启发的免疫克隆算法(QICA),其中抗体增殖被划分为一组子种群。子种群中的抗体由多态基因量子比特表示。抗体更新通过量子旋转门策略和动态角度调整机制实现,以加速收敛,量子变异通过量子非门实现,以避免过早收敛,并且设计了量子重组算子用于子种群之间的信息交流,从而提高搜索效率。同年,Li 等人提出了一种量子启发的免疫克隆多目标优化算法(QICMOA)。该算法使用量子比特对优势种群抗体进行编码,并设计量子重组算子和量子非门,以较少的拥挤密度克隆、重组和更新优势抗体。2013年,Liu 等人提出了一种文化免疫量子进化算法(CIQEA),该算法由基于 QEA 的种群空间和基于免疫接种的信念空间组成。种群空间定期向有信心的种群提供疫苗。信念空间不断进化这些疫苗,并优化种群空间的进化方向,从而大大提高了全局优化能力和收敛速度。2014年,Shang 等人提出了一种用于动态多目标优化(DMO)的免疫克隆协同进化算法(ICCoA)。该算法基于人工免疫系统的基本原理,通过免疫克隆选择方法解决 DMO 问题,并设计了协同进化竞争和合作算子,以提高解的一致性和多样性。2018年,Shang 等人提出了一种量子启发的免疫克隆算法(QICA-CARP)。该算法将种群中的抗体编码为量子比特,并通过当前最优抗体信息控制种群进化到一个良好的模式。量子变异策略和量子交叉算子加速了算法的收敛以及个体信息的交换。
5.3.4 量子种群优化
2005年,Alba 和 Dorronsoro 将网格种群结构细分为方块、矩形和条形,并设计了一种量子进化算法,引入了个体适应度与种群熵之间关系的预编程变化,以动态调整种群结构并构建第一个自适应动态细胞模型。2008年,Li 等人使用了一种新颖的距离测量方法来保持性能。该算法通过非支配排序方法进化解的种群,并使用 Pareto 最大-最小距离来保持种群多样性,从而在全局搜索和局部搜索之间实现良好的平衡。
2009年,Mohammad 和 Reza 提出了量子进化算法(QEA)中一种种群成员之间的动态结构化交互算法。该算法将 QEA 的种群结构分为环形结构、细胞结构、二叉树结构、簇结构、格子结构、星形结构和随机结构,并通过比较多种结构证明了细胞结构是 QEA 的最佳结构。
2015年,Qi 和 Xu 提出了一种基于 L5 的同步细胞量子进化算法(LSCQEA)。在 LSCQEA 算法中,每个个体位于一个格子中,并且格子中的每个个体及其四个相邻个体都经历一次 QEA 的迭代。在每次 QEA 迭代中,不同的个体通过与相邻个体的重叠交换信息,使种群不断进化。
2018年,Mei 和 Zhao 提出了一种随机扰动量子粒子群优化算法(RPQPSO)。通过引入随机扰动策略到迭代优化中,该算法能够动态自适应地调整,从而提高了局部搜索能力和全局搜索能力。
6 顶尖开放问题
物理知识的规律多样且强大,人工智能模型模拟了由数百万个通过权重连接的神经元组成的大脑,从而实现人类行为。通过物理知识与人工智能的结合、相互影响和演化,促进了人们对深度神经网络模型的理解,进而推动了新一代人工智能的发展。然而,将两者结合起来也面临着巨大的挑战,我们将围绕以下问题进行讨论(见图18)。
6.1 开放问题1:物理先验的可信性、可靠性和可解释性
作为一种通用模型,人工智能中的神经网络在物理学的各个领域变得越来越受欢迎(Redmon 等,2016;He 等,2017;Bahdanau 等,2014)。然而,神经网络的内在特性(如参数和模型推理结果等)难以解释,因此神经网络经常被贴上“黑箱”的标签。可解释性旨在以人类能够理解的方式描述系统的内部结构和推理,这与人脑的认知、感知和偏见密切相关。如今,新兴且活跃的物理神经网络交叉领域试图通过基于物理知识设计深度神经网络来使黑箱透明化。通过使用这种先验知识,更深更复杂的神经网络成为可能。然而,神经网络内部结构的推理和解释仍然是一个谜,作为先验知识补充的物理信息方法在解释人工智能神经网络时已成为一大挑战。
6.2 开放问题2:因果推理与决策制定
人工智能的目标是让机器学会像大脑一样“思考”和“决策”,而大脑对现实世界的理解、对不完全信息的处理以及在复杂场景中的任务处理能力是当前人工智能技术所无法比拟的,尤其是在时间序列问题上(Rubin,1974;Pearl,2009;Imbens 和 Rubin,2015)。由于大多数现有的人工智能模型是由关联驱动的,就像物理机器的决策输出会受到机制变化或其他因素干预的影响一样,这些模型通常只知道“如何”(关联)而不知道“为什么”(因果)。最近在时间序列因果性方面的突破性工作(Runge,2018;Runge 等,2019a,b;Nauta 等,2019)为人工智能奠定了基础。将因果推理、统计物理思维以及大脑的多视角认知活动引入人工智能领域,去除虚假关联,并利用因果推理和先验知识指导模型学习,是人工智能在未知环境中提高泛化能力的重大挑战。
6.3 开放问题3:灾难性遗忘
大脑记忆存储系统是一个信息过滤器,就像计算机清理磁盘空间一样,它可以删除数据中的无用信息以接收新信息。在神经生物学术语中,“灾难性遗忘”是指在学习新任务时,随着网络的加深,神经元之间的连接权重会减弱甚至消失。也就是说,新神经元的出现会导致权重重置,大脑中的海马体神经元重新连接并覆盖记忆(Abraham 和 Robins,2005)。对于人类来说,遗忘的发生可以通过减少过时信息对人们的影响来提高决策的灵活性,还可以让人们忘记负面事件,提高适应能力。
要实现今天的人工智能,代理必须能够学习和记住许多不同的任务,而学习过程最重要的部分是遗忘(McCloskey 和 Cohen,1989;Goodfellow 等,2013)。通过选择性遗忘的净化(Kirkpatrick 等,2017;Zhang 等,2023),人工智能可以更好地理解人类指令,提高算法的泛化能力,防止模型过拟合,并解决更多实际问题。因此,学习遗忘是人工智能面临的重大挑战之一。
6.4 开放问题4:知识与数据驱动的优化与协作
在解决许多实际优化问题时,由于它们具有非凸或多模态、大规模、高约束、多目标和约束的不确定性大等特点,难以解决,大多数进化优化算法评估候选解的潜力。目标函数和约束函数过于简单,可能不存在。相比之下,通过数值模拟、物理实验、生产过程或日常生活中收集的数据来评估目标和/或约束从而解决进化优化问题被称为数据驱动的进化优化。然而,数据驱动的优化算法也根据数据的性质(分布、噪声、异质性或动态性)带来了不同的挑战。受人工智能算法的启发,物理信息模型不仅降低了实现和计算成本(Belbute-Peres 等,2020),还具有更强的泛化能力(Sanchez-Gonzalez 等,2020)。人工智能主要基于知识库和推理引擎来模拟人类行为,而知识作为数据和信息的高度浓缩体现,往往意味着更高的算法执行效率。受物理学启发,知识驱动的人工智能具有丰富的经验和强大的可解释性,因此知识-数据双驱动优化协作为通用人工智能提供了一种新的方法和范式,将两者结合起来将是一个非常具有挑战性的课题。
6.5 开放问题5:物理信息数据扩充
在现实生活中,真实数据与预测数据分布之间存在差异,获得高质量的标注数据至关重要,因此迁移学习(Tremblay 等,2018;Bousmalis 等,2018)、多任务学习和强化学习是引入物理先验知识不可或缺的工具。
在现实中,许多问题无法独立分解为子问题,即使可以分解,每个子问题之间也通过某些共享因素或共享表示连接。因此,问题被分解为多个独立的单任务处理,忽略了问题中丰富的关联信息。多任务学习将多个相关任务放在一起进行学习,并在任务之间共享已学习的信息,这是单任务学习所不具备的。关联多任务学习(Thanasutives 等,2021)可以比单任务学习实现更好的泛化。然而,任务之间的干扰、不同任务之间的学习速率和损失函数以及模型表达能力的有限性,使得多任务学习在人工智能领域具有挑战性。
强化学习是人工智能领域中强调如何根据环境采取行动以最大化预期收益的领域。它带来的推理能力是人工智能的关键特征测量,它赋予机器自学和思考的能力。物理定律是先验知识,如何将强化学习与物理学相结合是一个具有挑战性的课题。
6.6 开放问题6:系统稳定性
在物理学中,稳定性是所有自动控制系统必须满足的性能指标。它是系统在受到干扰后能够恢复到原始平衡状态的性能。在人工智能领域,系统稳定性的研究是指系统的输出值能否跟上预期值,即分析系统输出值的稳定性(Chen 等,2023)。但是,由于人工智能系统具有动态系统的特性,输出值也具有动态特性。神经网络模型是生物神经系统的高度简化近似,即神经网络可以近似任何函数。从系统的角度来看,神经网络等同于系统的输出函数,即系统的动态系统。它模拟了人脑神经系统结构、机器信息处理、存储和检索的不同程度和层次的功能。从因果关系的角度来看,可解释性和稳定性之间存在一定的内部关系,即通过优化模型的稳定性,可以提高其可解释性,从而解决人工智能技术在实施过程中面临的当前困难。
作为一种新的学习范式,稳定学习试图结合这两个方向之间的共识基础。如何合理地放宽严格的假设以匹配更具挑战性的现实应用场景,使机器学习在不牺牲预测能力的情况下更可信,是未来稳定学习需要解决的关键问题。
6.7 开放问题7:轻量级网络
深度学习现在在人工智能领域发挥着重要作用,但受限于传统计算机架构,数据存储和计算需要通过存储芯片和中央处理单元完成,导致计算机处理数据时消耗时间长、能耗高等问题。将物理先验知识引入NAS的搜索空间,以获得最佳知识,从而在网络结构和预测结果之间取得平衡(Skomski 等,2021)。同时,模块化在基于物理知识的NAS中也起着关键作用(Xu 等,2019;Chen 等,2020;Goyal 等,2019)。深度神经网络结构复杂,涉及大量超参数,在训练过程中非常耗时耗能,并且难以并行化。因此,我们应结合大脑的物理结构和思维行为,加入物理先验知识,突破计算能力瓶颈,实现低功耗、低参数、高速度、高精度的非深度人工智能模型,开发更高效的人工智能技术。
6.8 开放问题8:物理信息联邦学习
隐私保护:人工智能算法的广泛应用不仅给人们带来了便利,也带来了巨大的隐私泄露风险。海量数据是人工智能的基础,正是由于大数据的使用、计算能力的提升以及算法的突破,AI才能快速发展并被广泛应用。获取和处理大量信息数据不可避免地涉及个人隐私保护的重要问题(Wang 和 Yang,2024)。因此,人工智能需要在隐私保护和AI能力之间找到平衡。
安全智能:随着人工智能在各行各业的广泛应用,滥用或恶意破坏人工智能系统将对社会产生巨大的负面影响。近年来,针对人工智能算法的算法攻击、对抗样本攻击、模型窃取攻击等攻击技术不断发展,这为人工智能带来了更大的算法安全风险。因此,实现人工智能的安全智能是未来的一大挑战。
6.9 开放问题9:算法公平性
尽管人工智能领域的快速发展为人们带来了诸多益处,但也存在一些公平性问题。如统计(采样)偏差、算法自身的敏感性以及人为偏见引入的歧视行为(Pfeiffer 等,2023)。作为人类决策的重要辅助工具,提高人工智能算法的公平性是人工智能领域广泛关注的问题(Xivuri 和 Twinomurinzi,2021)。考虑到物理距离和数据的大规模性,提高数据集质量、改善算法对敏感属性的依赖性(引入公平性约束)、定义指标量化和公平性测量,以及提高算法的泛化能力是重要的解决方案(Chen 等,2023)。此外,人机共生和算法透明性也是实现公平的重要途径。机器智能与人类大脑认知、思维和决策的人机共生,再加上对现实世界物理知识的归纳推理,将是未来的发展方向,而算法透明性(可理解性和可解释性)是实现公平的重要工具。算法公平性的问题不在于解决某些复杂的统计魔方难题,而在于尝试在只能捕捉影子的洞穴墙壁上体现柏拉图式的公平。因此,算法公平性研究的不断深入是人工智能治理的关键问题。
6.10 开放问题10:开放环境自适应学习
当今人工智能领域的假设都是关于封闭环境的,如数据的独立同分布(iid.)和分布常数假设。而在现实中,这是一个开放的动态环境,并且可能会发生变化。神经网络的学习环境是学习过程的必要条件。开放环境作为学习的一种机制,需要进行信息交换,这要求未来的人工智能具备适应环境的能力,或者说具备AI的鲁棒性。例如,在自动驾驶领域(Müller 等,2018),现实世界中总会出现训练样本无法模拟的紧急情况,尤其是在罕见场景下。因此,未来人工智能的发展必须能够克服数据分析和建模中的“开放环境”问题,这对人工智能系统的适应性或鲁棒性提出了巨大的挑战。
6.11 开放问题11:绿色低碳
随着人工智能领域的发展,人工智能赋能的产业逐渐需要一个更加绿色低碳的环境(Liu 和 Zhou,2024)。目前,人工智能的三大基石——算法、数据和计算能力正在大规模发展,导致资源消耗越来越高。因此,要实现绿色低碳智能,就必须进行“减法”(Yang 等,2024)。与此同时,新能源汽车、智能能源和人工智能的深度融合也对绿色低碳智能提出了巨大挑战。一方面,构建更灵活的网络模型;另一方面,构建更高效、更广泛的共享和再利用机制,从宏观角度实现绿色低碳。总之,“创新、协调、绿色、开放和共享”五大发展理念为未来人工智能的发展指明了方向,并提出了基本的遵循原则。
6.12 开放问题12:道德和伦理建设
目前,人工智能为人类创造了可观的经济利益,但其应用带来的负面影响和伦理问题也日益突出。可预测、受约束和行为导向的人工智能治理已成为人工智能时代的优先命题。例如,用户数据和信息的隐私保护;知识成果和算法的保护,人工智能换脸技术对肖像权的过度需求,以及自动驾驶安全事故的责任追究等问题。人工智能技术也可能被不法分子滥用,例如从事网络犯罪、制作和传播虚假新闻、合成足以干扰视听的虚假图像。人工智能应以保护用户隐私为发展原则。只有这样,人工智能的发展才能回馈人类,并为人与人工智能之间的新伦理提供新的希望(Akinrinola 等,2024)。
7 结论与展望
经过漫长时间的物理学演变,知识规律变得多样且强大。然而,我们当前对理论的理解不可避免地只是冰山一角。随着人工智能领域的发展,深度学习领域与物理学领域之间的联系日益紧密。将物理知识与人工智能相结合,不仅是推动物理概念进步的动力,也促进了新一代人工智能的发展。本文首先介绍了物理与人工智能的机制,然后对受物理启发的深度学习进行了相应的概述,主要包括经典力学、电磁学、统计物理学和量子力学对深度学习的启发,并阐述了深度学习如何解决物理问题。最后,讨论了受物理启发的人工智能所面临的挑战及对未来的思考。通过人工智能与物理学的跨学科分析和设计,探索更强大、更稳健的算法,以发展新一代人工智能。
元宇宙与人工智能三十人论坛
因微信公众号整改,没有加“星标⭐️ ”的订阅号有时无法收到消息
1.为防止错过最新资讯,请将元宇宙与人工智能三十人论坛设为星标⭐️
2.点击“赞”和“在看”,提高我们相遇的几率。
3.精彩文章,请点击文末左下角“分享”给好友。
了解更多关注


